题目内容
【题目】已知数列{an}满足an+1=﹣an2+2an ， n∈N* ， 且a1=0.9，令bn=lg（1﹣an）；
（1）求证：数列{bn}是等比数列；
（2）求数列{ 
}各项和．
【答案】
（1）证明：∵数列{an}满足an+1=﹣an2+2an，n∈N*，
∴1﹣an+1= 
，且a1=0.9，1﹣a1=0.1．
对1﹣an+1= 两边取对数可得：lg（1﹣an+1）=2lg（1﹣an），
∵bn=lg（1﹣an），∴bn+1=2bn．
∴数列{bn}是等比数列，公比为2，首项为﹣1
（2）解：由（1）可得：bn=﹣2n﹣1．
=﹣ 
．
∴数列{ }各项和= 
= 
=﹣2
【解析】（1）数列{an}满足an+1=﹣an2+2an ， n∈N* ， 变形为1﹣an+1= ，两边取对数可得：lg（1﹣an+1）=2lg（1﹣an），可得：bn+1=2bn ． 即可证明．（2）由（1）可得：bn=﹣2n﹣1. =﹣ ．再利用无穷等比数列的求和公式即可得出．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系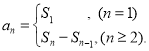
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案【题目】【2017北京西城区5月模拟】某大学为调研学生在
，
两家餐厅用餐的满意度，从在
，
两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分.
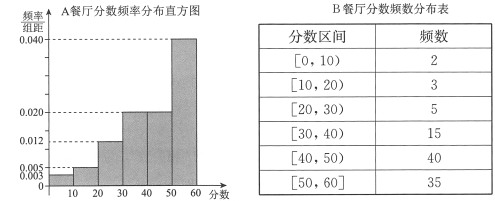
整理评分数据，将分数以10为组距分成6组：
，
，
，
，
，
，得到
餐厅分数的频率分布直方图，和
餐厅分数的频数分布表：
定义学生对餐厅评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 |
|
|
|
（Ⅰ）在抽样的100人中，求对
餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在
，
两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对
餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从
，
两家餐厅中选择一家用餐，你会选择哪一家？说明理由.
