题目内容
已知函数x,y满足x≥1,y≥1 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围. 当a>1时,logaxy的最大值为2+2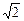 ,最小值为1+
,最小值为1+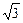 ;
;
当0<a<1时,logaxy的最大值为1-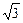 ,最小值为2-2
,最小值为2-2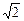 .
.
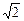 ,最小值为1+
,最小值为1+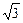 ;
;当0<a<1时,logaxy的最大值为1-
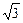 ,最小值为2-2
,最小值为2-2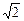 .
. 由已知等式得 loga2x+loga2y=(1+2logax)+(1+2logay),
loga2x+loga2y=(1+2logax)+(1+2logay),
即(logax-1)2+(logay-1)2="4, "
令u=logax,v=logay,k=logaxy,则(u-1)2+(v-1)2=4(uv≥0),k=u+v.
在直角坐标系uOv内,
圆弧(u-1)2+(v-1)2=4(uv≥0)与平行直线系v=-u+k有公共点,
分两类讨论:
(1)当u≥0,v≥0时,即a>1时,结合判别式法与代点法得
1+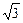 ≤k≤2(1+
≤k≤2(1+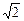 );
);
(2)当u≤0,v≤0,即0<a<1时,同理得到2(1-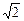 )≤k≤1-
)≤k≤1-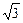 .
.
综上,当a>1时,logaxy的最大值为2+2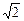 ,最小值为1+
,最小值为1+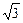 ;
;
当0<a<1时,logaxy的最大值为1-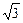 ,最小值为2-2
,最小值为2-2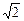 .
.
 loga2x+loga2y=(1+2logax)+(1+2logay),
loga2x+loga2y=(1+2logax)+(1+2logay),即(logax-1)2+(logay-1)2="4, "
令u=logax,v=logay,k=logaxy,则(u-1)2+(v-1)2=4(uv≥0),k=u+v.
在直角坐标系uOv内,
圆弧(u-1)2+(v-1)2=4(uv≥0)与平行直线系v=-u+k有公共点,
分两类讨论:
(1)当u≥0,v≥0时,即a>1时,结合判别式法与代点法得
1+
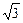 ≤k≤2(1+
≤k≤2(1+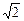 );
);(2)当u≤0,v≤0,即0<a<1时,同理得到2(1-
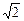 )≤k≤1-
)≤k≤1-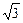 .
. 综上,当a>1时,logaxy的最大值为2+2
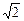 ,最小值为1+
,最小值为1+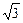 ;
;当0<a<1时,logaxy的最大值为1-
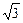 ,最小值为2-2
,最小值为2-2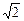 .
. 
练习册系列答案
相关题目
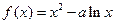 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且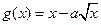 在区间[0,1]上是减函数。
在区间[0,1]上是减函数。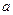 的值;
的值;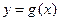 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线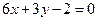 距离的最小值;
距离的最小值; 且
且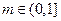 时,
时,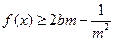 恒成立,求
恒成立,求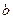 的取值范围。
的取值范围。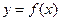 的反函数为
的反函数为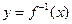 ,定义:若对给定的实数
,定义:若对给定的实数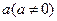 ,函数
,函数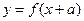 与
与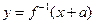 互为反函数,则称
互为反函数,则称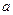 和性质”.
和性质”.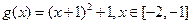 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由; 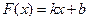 ,其中
,其中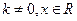 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得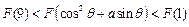 对任意的
对任意的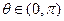 恒成立?若存在,求出
恒成立?若存在,求出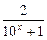 -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像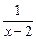 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x). 
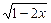 的值域是( )
的值域是( )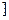
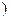
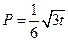 ,
,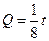 .今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
.今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).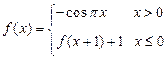 ,则
,则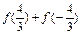 的值等于
的值等于