题目内容
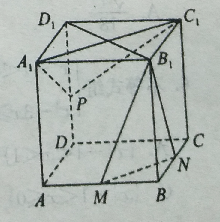
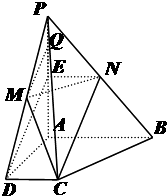
【题目】已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形, ∠CDA=∠BAD=90°, ![]() ,M,N分别是PD,PB的中点.
,M,N分别是PD,PB的中点.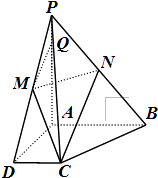
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
【答案】
(1)解:法一向量法:
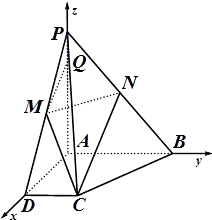
以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O﹣xyz,
由 ![]() ,PA=4PQ=4,M,N分别是PD,PB的中点,
,PA=4PQ=4,M,N分别是PD,PB的中点,
可得: ![]() ,
,
∴ ![]() ,
, ![]()
设平面的PBC的法向量为 ![]() ,
,
则有: 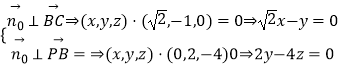
令z=1,则 ![]() ,
,
∴ ![]() ,
,
又MQ平面PCB,∴MQ∥平面PCB
法二,几何法:
取AP的中点E,连接ED,则ED∥CN,依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,
又MQ平面PCB,CN平面PCB,∴MQ∥平面PCB
(2)解:设平面的MCN的法向量为 ![]() ,又
,又 ![]()
则有: 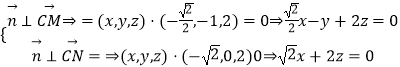
令z=1,则 ![]() ,
,
又 ![]() 为平面ABCD的法向量,
为平面ABCD的法向量,
∴ 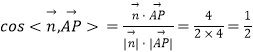 ,又截面MCN与底面ABCD所成二面角为锐二面角,
,又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为 ![]()
法二,几何法:
易证:平面MEN∥底面ABCD,所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的二面角,
因为PA⊥平面ABCD,所以PA⊥平面MEN,过E做EF⊥MN,垂足为F,连接QF,
则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面所以∠QFE为截面MCN与平面MEN所成的二面角的平面角, ![]() ,
,
所以: ![]() ,
,
所以: ![]()
(3)解:∵ ![]() ,∴所求的距离
,∴所求的距离 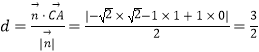
法二,几何法:
因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,
由(2)知:MN⊥平面QEF,则平面MCNQ⊥平面QEF且交线为QF,作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.
![]()
【解析】此类题一般有两种解法,一种是利用空间向量法来证明,一种是用立体几何中线面位置关系进行证明,本题提供两种解法 向量法:对于(1)求证:MQ∥平面PCB,可求出线的方向向量与面的法向量,如果两者的内积为0则说明线面平行对于(2)求截面MCN与底面ABCD所成二面角的大小,求出两个平面的法向量,然后根据根据二面角的正弦与法向量的数量积的关系,求解;对于(3)求点A到平面MCN的距离,求出平面上任一点与A连线所对应的向量,求这个向量在该平面的法向量上的投影即可,此法求点到面的距离甚为巧妙.几何法:(1)求证MQ∥平面PCB,用线面平行的判定定理证明即可;(2)求截面MCN与底面ABCD所成二面角的大小,先在图形中作出二面角的平面角,再证明其是二面角的平面角,然后根据题设中的条件求出平面角的三角函数值,一般要在一个三角形中求解函数值.(3)求点A到平面MCN的距离,须先作出点A在面上的垂线段,然后在三角形中求出此线段的长度即可.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 快捷英语周周练系列答案
快捷英语周周练系列答案