Question

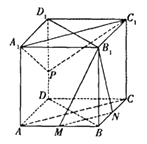
【题目】如图，正方体 中， 分别为 的中点.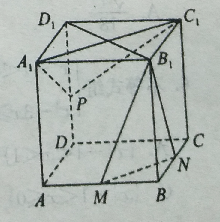

（1）求证:平面 ⊥平面 ；
（2）当点 在 上运动时，是否都有 平面 ，证明你的结论；
（3）若 是 的中点，试判断 与平面 是否垂直？请说明理由.

Answer 1

【答案】
（1）证明：正方体 中， 平面 ，

平面 ，所以 ，

连接 ，因为 分别为 的中点，

所以 ,

又四边形 是正方形，所以 ，所以 ，

因为 ，所以 平面 ，

又因为 平面 ，所以平面 平面 ，

（2）解：当点 在 上移动时，都有 平面 ，证明如下：

在正方体中 ，A1A∥C1C，且A1A=C1C，所以A1ACC1为平行四边形，

所以A1 C1∥A C，

由（1）知，MN∥A C，所以MN∥A1 C1

又

所以

（3）解：PB⊥平面B1MN
设 的中点为Q，连接PQ，则PQ⊥平面 B1B

再连接BQ，因为Q，M分别为 ，AB的中点

所以△BB1M≌△ABQ

所以∠BB1M=∠ABQ，所以∠ABQ+∠BMB1=90°

所以B1M⊥BQ，又PQ⊥平面 B1B,所以PQ⊥B1M

所以B1M⊥平面PBQ

所以B1M⊥PB，又由（1）知， MN⊥平面BB1D1D,所以MN⊥PB

所以PB⊥平面B1MN

【解析】（1）根据题意作出辅助线结合已知可得 M N / / A C即 M N ⊥ B D ，利用线面垂直的判定定理可得出M N ⊥ 平面 B B1 D1 D，进而由面面垂直的判定定理即可得证。（2）当当点 P 在 D1 D 上运动时，都有 M N / / 平面 A1 C 1P.利用线面平行的判定定理即可证明。（3)要证明PB⊥平面B1MN需利用题设条件推导出B1M⊥BQ，PQ⊥B1M，由此能够证明PB⊥平面B1MN成立。
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．