题目内容
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
B.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
C.f(0)>2f( ![]() )
)
D.f(0)> ![]() f(
f( ![]() )
)
【答案】A
【解析】解:构造函数g(x)= ![]() , 则g′(x)=
, 则g′(x)= ![]() =
= ![]() (f′(x)cosx+f(x)sinx),
(f′(x)cosx+f(x)sinx),
∵对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0,
)满足f′(x)cosx+f(x)sinx>0,
∴g′(x)>0,即函数g(x)在x∈(﹣ ![]() ,
, ![]() )单调递增,
)单调递增,
则g(﹣ ![]() )<g(﹣
)<g(﹣ ![]() ),即
),即 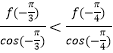 ,
,
∴ 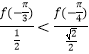 ,即
,即 ![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() ),故A正确.
),故A正确.
g(0)<g( ![]() ),即
),即 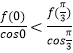 ,
,
∴f(0)<2f( ![]() ),
),
故选:A.
根据条件构造函数g(x)= ![]() ,求函数的导数,利用函数的单调性和导数之间的关系即可得到结论.
,求函数的导数,利用函数的单调性和导数之间的关系即可得到结论.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
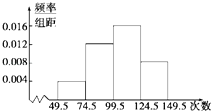
【题目】某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | a | b |
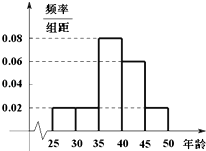
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.