题目内容
【题目】货车欲以xkm/h的速度行驶,去130km远的某地,按交通法规,限制x的允许范围是50≤x≤100,假设汽油的价格为2元/升,而汽车耗油的速率是![]() 升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
【答案】最经济的车速是57km/h,这次行车往返的总费用最低约为2×82.2=164.4(元).
【解析】
求出单程行驶:汽车运行的时间为小时![]() ,耗油量为
,耗油量为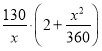 升,耗油费用为
升,耗油费用为 元,司机的工资为
元,司机的工资为![]() 元,推出这次行车的单程费用利用函数的导数求解函数的最值即可
元,推出这次行车的单程费用利用函数的导数求解函数的最值即可
单程行驶:汽车运行的时间为![]() 小时,耗油量为
小时,耗油量为![]() ·
·![]() 升,耗油费用为2·
升,耗油费用为2·![]() ·
·![]() 元,司机的工资为14×
元,司机的工资为14×![]() 元,
元,
故这次行车的单程费用为
y=2·![]() ·
·![]() +14·
+14·![]() =130·
=130·![]() .
.
所以y′=130·![]() .
.
令y′=0得,x=18![]() ≈57(km/h),当50≤x<18
≈57(km/h),当50≤x<18![]() 时,
时,![]() ,y单调递减;
,y单调递减;
当18![]() ≤x≤100时,
≤x≤100时,![]() ,y单调递增,
,y单调递增,
当x=18![]() 时,y取得最小值,
时,y取得最小值,
即所以y=130×![]() ≈82.2(元).所以最经济的车速是57 km/h,这次行车往返的总费用最低约为2×82.2=164.4(元).
≈82.2(元).所以最经济的车速是57 km/h,这次行车往返的总费用最低约为2×82.2=164.4(元).

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目