题目内容
【题目】在平面直角坐标系![]() 中,己知圆
中,己知圆![]() ,且圆
,且圆![]() 被直线
被直线![]() 截得的弦长为2.
截得的弦长为2.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 的切线
的切线![]() 在
在![]() 轴和
轴和![]() 轴上的截距相等,求切线
轴上的截距相等,求切线![]() 的方程;
的方程;
(3)若圆![]() 上存在点
上存在点![]() ,由点
,由点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)将圆方程整理为标准方程形式,可知![]() ,得到圆心坐标和半径;由垂径定理可利用弦长构造出关于
,得到圆心坐标和半径;由垂径定理可利用弦长构造出关于![]() 的方程,解方程求得
的方程,解方程求得![]() ,从而得到标准方程;(2)分为直线
,从而得到标准方程;(2)分为直线![]() 过原点和不过原点两种情况,分别假设直线方程,利用圆心到直线距离等于半径可构造方程求得结果;(3)设
过原点和不过原点两种情况,分别假设直线方程,利用圆心到直线距离等于半径可构造方程求得结果;(3)设![]() ,根据
,根据![]() 且
且![]() 可整理出
可整理出![]() 点轨迹方程为:
点轨迹方程为:![]() ;根据
;根据![]() 在圆
在圆![]() 上,则两圆有公共点,根据圆与圆位置关系的判定可构造不等式,解不等式求得结果.
上,则两圆有公共点,根据圆与圆位置关系的判定可构造不等式,解不等式求得结果.
(1)圆![]() 方程可整理为:
方程可整理为:![]()
![]()
![]() 圆
圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径
,半径![]()
![]() 圆心
圆心![]() 到直线
到直线![]() 的距离:
的距离: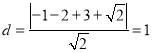
![]() 截得的弦长为:
截得的弦长为:![]() ,解得:
,解得:![]()
![]() 圆
圆![]() 的标准方程为:
的标准方程为:![]()
(2)①若直线![]() 过原点,可假设直线
过原点,可假设直线![]() 方程为:
方程为:![]() ,即
,即![]()
![]() 直线
直线![]() 与圆相切
与圆相切 ![]() 圆心到直线距离
圆心到直线距离![]() ,解得:
,解得:![]()
![]() 切线
切线![]() 方程为:
方程为:![]()
②若直线![]() 不过原点,可假设直线
不过原点,可假设直线![]() 方程为:
方程为:![]() ,即
,即![]()
![]() 圆心到直线距离
圆心到直线距离![]() ,解得:
,解得:![]() 或
或![]()
![]() 切线
切线![]() 方程为
方程为![]() 或
或![]()
综上所述,切线![]() 方程为
方程为![]() 或
或![]() 或
或![]()
(3)假设![]()
![]() ,即
,即![]()
又直线![]() 与圆
与圆![]() 相切,切点为
相切,切点为![]()
![]()
即:![]() ,整理得:
,整理得:![]()
![]() 又在圆
又在圆![]() 上
上 ![]() 两圆有公共点
两圆有公共点
![]() ,解得:
,解得:![]()
即![]() 的取值范围为:
的取值范围为:![]()

练习册系列答案
相关题目