题目内容
【题目】某人承揽一项业务，需做文字标牌4个，绘画标牌5个，现有两种规格的原料，甲种规格每张3m2，可做文字标牌1个，绘画标牌2个，乙种规格每张2m2，可做文字标牌2个，绘画标牌1个，求两种规格的原料各用多少张，才能使总的用料面积最小？
【答案】使用甲种规格原料2张，乙种规格原料1张，可使总的用料面积最小．
【解析】
本题考查的知识点是简单的线性规划的应用，根据已知条件中解：需要甲种原料x张，乙种原料y张，则可做文字标牌（x+2y）个，绘画标牌（2x+y）个，由题意得出约束条件，及目标函数，然后利用线性规划，求出最优解．
解：设需要甲种原料x张，乙种原料y张，
则可做文字标牌（x+2y）个，绘画标牌（2x+y）个．
由题意可得：
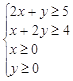
所用原料的总面积为z=3x+2y，作出可行域如图，
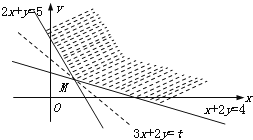
在一组平行直线3x+2y=t中，经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点（2，1），∴最优解为：x=2，y=1
∴使用甲种规格原料2张，乙种规格原料1张，可使总的用料面积最小．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
