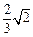题目内容
如图所示,离心率为 的椭圆
的椭圆 上的点到其左焦点的距离的最大值为3,过椭圆
上的点到其左焦点的距离的最大值为3,过椭圆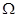 内一点
内一点 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 、
、 和
和 、
、 ,且满足
,且满足 ,其中
,其中 为常数,过点
为常数,过点 作
作 的平行线交椭圆于
的平行线交椭圆于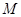 、
、 两点.
两点.

(1)求椭圆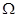 的方程;
的方程;
(2)若点 ,求直线
,求直线 的方程,并证明点
的方程,并证明点 平分线段
平分线段 .
.
 的椭圆
的椭圆 上的点到其左焦点的距离的最大值为3,过椭圆
上的点到其左焦点的距离的最大值为3,过椭圆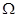 内一点
内一点 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 、
、 和
和 、
、 ,且满足
,且满足 ,其中
,其中 为常数,过点
为常数,过点 作
作 的平行线交椭圆于
的平行线交椭圆于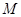 、
、 两点.
两点.
(1)求椭圆
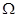 的方程;
的方程;(2)若点
 ,求直线
,求直线 的方程,并证明点
的方程,并证明点 平分线段
平分线段 .
.(1) ;(2)详见解析.
;(2)详见解析.
 ;(2)详见解析.
;(2)详见解析.试题分析:(1)由题得
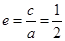 ,
, ,联立
,联立 解这个方程组即得.(2)首先求出直线MN的方程.由于MN过点P(1,1),故只要求出MN的斜率即可.又由于MN平行AB,故先求出直线AB的斜率.设
解这个方程组即得.(2)首先求出直线MN的方程.由于MN过点P(1,1),故只要求出MN的斜率即可.又由于MN平行AB,故先求出直线AB的斜率.设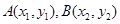 ,则
,则 .由
.由 可得点C的坐标,由
可得点C的坐标,由 可得点D的坐标,将A、B、C、D的坐标代入椭圆方程得四个等式,利用这四个等式可整体求出
可得点D的坐标,将A、B、C、D的坐标代入椭圆方程得四个等式,利用这四个等式可整体求出 ,然后求出直线MN的方程,与椭圆方程联立可求得MN的中点坐标即为点P的坐标,从而问题得证 .
,然后求出直线MN的方程,与椭圆方程联立可求得MN的中点坐标即为点P的坐标,从而问题得证 .(1)由题得
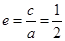 ,
, ,联立
,联立 解得
解得 ,
, ,
, ,
,∴椭圆方程为
 4分
4分(2)方法一:设
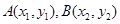 ,由
,由 可得
可得 .
.∵点
 在椭圆上,故
在椭圆上,故
整理得:
 6分
6分又点
 在椭圆上可知
在椭圆上可知 ,
,故有
 ①
①由
 ,同理可得:
,同理可得: ②
②②-①得:
 ,即
,即 9分
9分又
 ∥
∥ ,故
,故
∴直线
 的方程为:
的方程为: ,即
,即 .
.由
 可得:
可得:
∴
 是
是 的中点,即点
的中点,即点 平分线段
平分线段 12分
12分(2)方法二:∵
 ,
, ,∴
,∴ ,即
,即

在梯形
 中,设
中,设 中点为
中点为 ,
, 中点为
中点为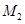 ,
,过
 作
作 的平行线交
的平行线交 于点
于点
∵
 与
与 面积相等,∴
面积相等,∴
∴
 ,
,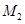 ,
, 三点共线 6分
三点共线 6分设
 ,
,
∴
 ,
, ,
, 两式相减得
 ,
,
显然
 ,(否则
,(否则 垂直于
垂直于 轴,因
轴,因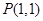 不在
不在 轴上,此时
轴上,此时 不可能垂直于
不可能垂直于 轴保持与
轴保持与 平行)且
平行)且 (否则
(否则 平行于
平行于 轴或经过原点,此时
轴或经过原点,此时 ,
,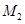 ,
, 三点不可能共线)
三点不可能共线)∴
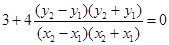
设直线
 斜率为
斜率为 ,直线
,直线 斜率为
斜率为
∴
 ,即
,即 ①
①设直线
 斜率为
斜率为 ,直线
,直线 斜率为
斜率为
同理,
 ,又
,又 ,∴
,∴ 即
即 三点共线 8分
三点共线 8分∴
 四点共线,∴
四点共线,∴ ,代入①得
,代入①得  9分
9分∴直线
 的方程为
的方程为  即
即
联立
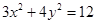 得
得
∴点
 平分线段
平分线段 12分
12分
练习册系列答案
相关题目
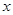 轴上的椭圆
轴上的椭圆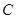 过点
过点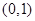 ,且离心率为
,且离心率为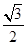 ,
,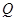 为椭圆
为椭圆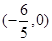 的直线
的直线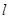 与椭圆
与椭圆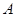 ,
,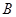 两点.
两点.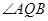 的大小;
的大小;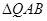 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线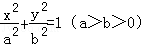 过点(0,4),离心率为
过点(0,4),离心率为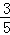
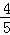 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.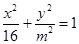 (m>0),如果直线y=
(m>0),如果直线y= x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
 上的点到直线
上的点到直线 的最大距离是 .
的最大距离是 . 过点
过点 和点
和点 .
. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆 两点,且
两点,且 ,求直线
,求直线 的左、右焦点,A、B是以O(O
的左、右焦点,A、B是以O(O B.
B. C.
C. D.
D.
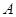 是椭圆
是椭圆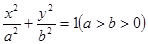 上一点,
上一点,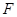 为椭圆的一个焦点,且
为椭圆的一个焦点,且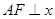 轴,
轴,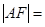 焦距,则椭圆的离心率是
焦距,则椭圆的离心率是  与椭圆
与椭圆 相交于
相交于 、
、 两点,若椭圆的离心率为
两点,若椭圆的离心率为 ,焦距为2,则线段
,焦距为2,则线段 的长是( )
的长是( )