题目内容
(12分)(2011•陕西)设椭圆C: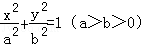 过点(0,4),离心率为
过点(0,4),离心率为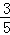
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为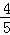 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
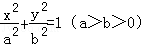 过点(0,4),离心率为
过点(0,4),离心率为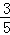
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为
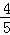 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.(Ⅰ)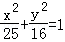 (Ⅱ)
(Ⅱ)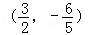
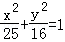 (Ⅱ)
(Ⅱ)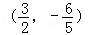
试题分析:(Ⅰ)根据题意,将(0,4)代入C的方程得b的值,进而由椭圆的离心率为
 ,结合椭圆的性质,可得
,结合椭圆的性质,可得 =
=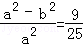 ;解可得a的值,将a、b的值代入方程,可得椭圆的方程.
;解可得a的值,将a、b的值代入方程,可得椭圆的方程.(Ⅱ)根据题意,可得直线的方程,设直线与C的交点为A(x1,y1),B(x2,y2),联立直线与椭圆的方程,化简可得方程x2﹣3x﹣8=0,解可得x1与x2的值,由中点坐标公式可得中点的横坐标,将其代入直线方程,可得中点的纵坐标,即可得答案.
解:(Ⅰ)根据题意,椭圆过点(0,4),
将(0,4)代入C的方程得
 ,即b=4
,即b=4又
 得
得 =
=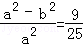 ;
;即
 ,∴a=5
,∴a=5∴C的方程为
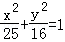
(Ⅱ)过点(3,0)且斜率为
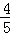 的直线方程为
的直线方程为 ,
,设直线与C的交点为A(x1,y1),B(x2,y2),
将直线方程
 代入C的方程,得
代入C的方程,得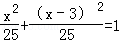 ,
,即x2﹣3x﹣8=0,解得
 ,
,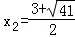 ,
,∴AB的中点坐标
 ,
, ,
,即中点为
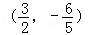 .
.点评:本题考查椭圆的性质以及椭圆与直线相交的有关性质,涉及直线与椭圆问题,一般要联立两者的方程,转化为一元二次方程,由韦达定理分析解决.

练习册系列答案
相关题目
 为椭圆
为椭圆 上两动点,
上两动点, 分别为其左右焦点,直线
分别为其左右焦点,直线 过点
过点 ,且不垂直于
,且不垂直于 轴,
轴, 的周长为
的周长为 ,且椭圆的短轴长为
,且椭圆的短轴长为 .
. 的标准方程;
的标准方程; 为椭圆
为椭圆 并延长交直线
并延长交直线 于点
于点 .求证:直线
.求证:直线 过定点.
过定点.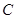 过点
过点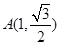 ,两焦点为
,两焦点为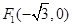 、
、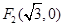 ,
,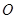 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线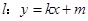 与椭圆交于两不同点
与椭圆交于两不同点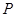 、
、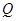 .
.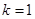 时,求
时,求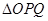 面积的最大值;
面积的最大值;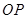 、
、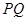 、
、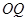 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线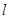 的斜率
的斜率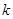 .
. 的椭圆
的椭圆 上的点到其左焦点的距离的最大值为3,过椭圆
上的点到其左焦点的距离的最大值为3,过椭圆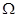 内一点
内一点 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 、
、 和
和 、
、 ,且满足
,且满足 ,其中
,其中 为常数,过点
为常数,过点 的平行线交椭圆于
的平行线交椭圆于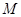 、
、 两点.
两点.
 ,求直线
,求直线 的方程,并证明点
的方程,并证明点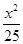 +
+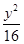 =1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.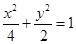 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )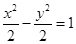



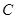 :
: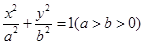 经过点
经过点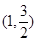 ,其离心率
,其离心率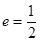 .
.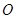 作不与坐标轴重合的直线
作不与坐标轴重合的直线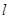 交椭圆
交椭圆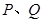 两点,过
两点,过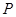 作
作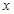 轴的垂线,垂足为
轴的垂线,垂足为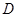 ,连接
,连接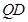 并延长交椭圆
并延长交椭圆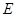 ,试判断随着
,试判断随着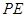 与
与 的一个焦点为
的一个焦点为 ,且离心率为
,且离心率为 .
.  的直线
的直线 过点
过点 ,且与椭圆交于
,且与椭圆交于 两点,
两点, 为直线
为直线 上的一点,若△
上的一点,若△ 为等边三角形,求直线
为等边三角形,求直线