题目内容
椭圆 上的点到直线
上的点到直线 的最大距离是 .
的最大距离是 .
 上的点到直线
上的点到直线 的最大距离是 .
的最大距离是 .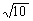
试题分析:∵椭圆方程为
 ∴可设椭圆上的任意一点P坐标为(4cosα,2sinα)∴P到直线
∴可设椭圆上的任意一点P坐标为(4cosα,2sinα)∴P到直线 的距离d=
的距离d= ∵?4
∵?4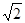 ≤
≤ ≤4
≤4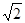 ∴
∴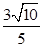 ≤
≤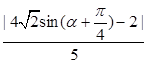 ≤
≤ ∴d的最大值为
∴d的最大值为 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 上的点到直线
上的点到直线 的最大距离是 .
的最大距离是 .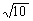
 ∴可设椭圆上的任意一点P坐标为(4cosα,2sinα)∴P到直线
∴可设椭圆上的任意一点P坐标为(4cosα,2sinα)∴P到直线 的距离d=
的距离d= ∵?4
∵?4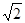 ≤
≤ ≤4
≤4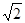 ∴
∴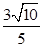 ≤
≤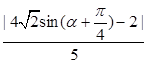 ≤
≤ ∴d的最大值为
∴d的最大值为 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案