题目内容
已知点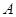 是椭圆
是椭圆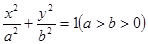 上一点,
上一点,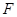 为椭圆的一个焦点,且
为椭圆的一个焦点,且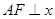 轴,
轴,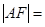 焦距,则椭圆的离心率是
焦距,则椭圆的离心率是
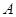 是椭圆
是椭圆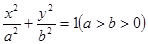 上一点,
上一点,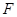 为椭圆的一个焦点,且
为椭圆的一个焦点,且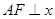 轴,
轴,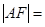 焦距,则椭圆的离心率是
焦距,则椭圆的离心率是 
试题分析:设焦点
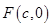 ,椭圆方程中令
,椭圆方程中令 得
得

 整理的
整理的 即
即


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
题目内容
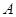 是椭圆
是椭圆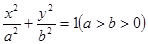 上一点,
上一点,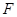 为椭圆的一个焦点,且
为椭圆的一个焦点,且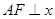 轴,
轴,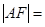 焦距,则椭圆的离心率是
焦距,则椭圆的离心率是 
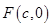 ,椭圆方程中令
,椭圆方程中令 得
得

 整理的
整理的 即
即


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案