题目内容
已知椭圆 过点
过点 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
 过点
过点 和点
和点 .
.(1)求椭圆
 的方程;
的方程;(2)设过点
 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.(1)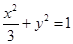 ;(2)
;(2)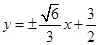
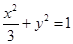 ;(2)
;(2)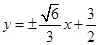
试题分析:(1)将两点代入椭圆方程可解得
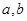 的值,从而可得椭圆的方程。(2)分析可知直线
的值,从而可得椭圆的方程。(2)分析可知直线 的斜率
的斜率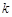 存在,且
存在,且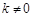 。设直线
。设直线 的方程为
的方程为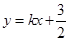 ,与椭圆方程联立消去
,与椭圆方程联立消去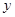 得关于
得关于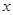 的一元二次方程,因为有两个交点故判别式应大于0.且可得根与系数的关系,从而可得
的一元二次方程,因为有两个交点故判别式应大于0.且可得根与系数的关系,从而可得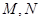 的中点坐标,因为
的中点坐标,因为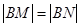 所以点
所以点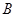 和
和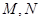 中点的连线垂直直线
中点的连线垂直直线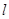 ,即两直线斜率之积等于
,即两直线斜率之积等于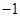 。从而可求得
。从而可求得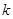 的值。
的值。解:(1)因为椭圆
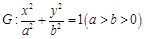 过点
过点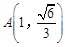 和点
和点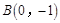 .
.所以
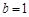 ,由
,由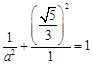 ,得
,得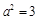 .
.所以椭圆
 的方程为
的方程为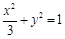 .
.(2)显然直线
 的斜率
的斜率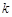 存在,且
存在,且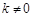 .设直线
.设直线 的方程为
的方程为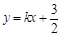 .
.由
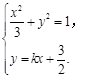 消去
消去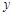 并整理得
并整理得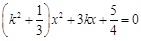 ,
,由
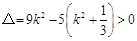 ,
,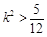 .
.设
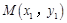 ,
,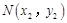 ,
,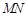 中点为
中点为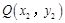 ,
,得
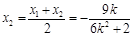 ,
,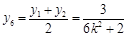 .
.由
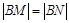 ,知
,知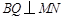 ,
,所以
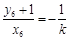 ,即
,即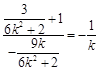 .
.化简得
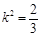 ,满足
,满足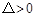 .
.所以
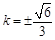 .
.因此直线
 的方程为
的方程为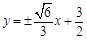 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的椭圆
的椭圆 上的点到其左焦点的距离的最大值为3,过椭圆
上的点到其左焦点的距离的最大值为3,过椭圆 内一点
内一点 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 、
、 和
和 、
、 ,且满足
,且满足 ,其中
,其中 为常数,过点
为常数,过点 的平行线交椭圆于
的平行线交椭圆于 、
、 两点.
两点.
 ,求直线
,求直线 的方程,并证明点
的方程,并证明点 的右焦点为F,P为椭圆上的一个动点.
的右焦点为F,P为椭圆上的一个动点. 时,求直线l的方程.
时,求直线l的方程. 的一个焦点为
的一个焦点为 ,且离心率为
,且离心率为 .
.  的直线
的直线 过点
过点 ,且与椭圆交于
,且与椭圆交于 两点,
两点, 为直线
为直线 上的一点,若△
上的一点,若△ 为等边三角形,求直线
为等边三角形,求直线 的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|=
的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|= ,直线L的斜率为1,则b的值为( )
,直线L的斜率为1,则b的值为( )



 ,左右焦点分别为
,左右焦点分别为 ,过
,过 的直线
的直线 交椭圆于A,B两点,若
交椭圆于A,B两点,若 的最大值为5,则
的最大值为5,则 的值是 ( )
的值是 ( )


 .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求 是椭圆
是椭圆 上的点,则
上的点,则 的取值范围是 .
的取值范围是 .