题目内容
(本题满分12分)
如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE.
(2)设点M为线段AB的中点,点N为线段

如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE.
(2)设点M为线段AB的中点,点N为线段

证明:(1)因为BC⊥平面ABE,AE?平面ABE, 所以AE⊥BC.
又BF⊥平面ACE,AE?平面ACE,所以AE⊥BF,
又BF∩BC=B,所以AE⊥平面BCE.
又BE?平面BCE,所以AE⊥BE. ……………………….6分
(2)取DE的中点P,连结PA、PN,因为点N为线段CE的中点,
所以PN∥DC,且PN=
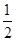 DC.
DC.又四边形ABCD是矩形,点M为线段AB的中点,
所以AM∥DC,且AM=
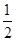 DC,
DC,所以PN∥AM,且PN=AM,故四边形AMNP是平行四边形,所以MN∥AP.
而AP?平面DAE,MN?平面DAE, 所以MN∥平面DAE. ……………………….12分
略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
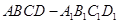 中,已知底面
中,已知底面 的边长为2,点P是
的边长为2,点P是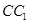 的中点,直线AP与平面
的中点,直线AP与平面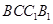 成
成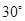 角.
角. 的长;
的长; 和AP所成角的大小.(结果用反三角函数值表示);
和AP所成角的大小.(结果用反三角函数值表示);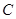 到平面
到平面 的距离.
的距离.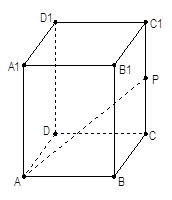
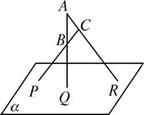
 是互不相同的空间直线,
是互不相同的空间直线,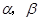 是不重合的平面,则下列命题中为真命题的是
是不重合的平面,则下列命题中为真命题的是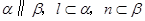 ,则
,则
 ,则
,则

 ,则
,则


 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径。
的直径。
 ,在圆柱
,在圆柱
 与平面
与平面 所成的角为
所成的角为
 ,当
,当 的值。
的值。
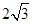 ,
,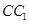 =
=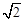 ,则二面角
,则二面角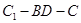 的大小为_______;
的大小为_______;