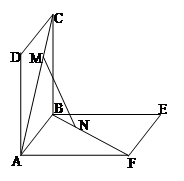题目内容
(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:(1) FD∥平面ABC; (2) AF⊥平面EDB.




∵ F、M分别是BE、BA的中点 ∴ FM∥EA, FM=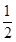 EA
EA
∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又 DC="a, " ∴ FM="DC " ∴四边形FMCD是平行四边形
∴ FD∥MC
FD∥平面ABC
(2) 因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB.
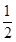 EA
EA∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又 DC="a, " ∴ FM="DC " ∴四边形FMCD是平行四边形
∴ FD∥MC
FD∥平面ABC
(2) 因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB.
略

练习册系列答案
相关题目
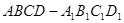 中,
中,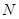 是
是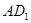 的中点,
的中点,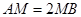 .
.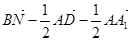 ;
;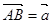 ,
,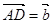 ,
,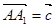 ,若
,若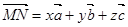 ,求
,求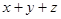 .
.

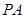 垂直于矩形
垂直于矩形 所在的平面,
所在的平面,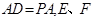 分别是
分别是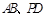 的中点.
的中点.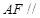 平面
平面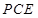 ;
;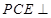 平面
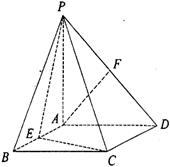
平面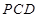 .
. 
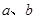 是异面直线,直线
是异面直线,直线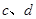 分别与
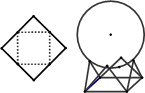
分别与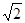 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其 中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其 中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )