题目内容
【题目】已知圆
.
（1）求证：对任意实数
，该圆恒过一定点；
（2）若该圆与圆
外切，求
的值.
【答案】（1）详见解析（2）
【解析】
试题分析：（1）将a分离，可得
，对任意实数a成立，则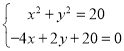
，由此可得结论；（2）利用两圆外切，内切，分别求出a的值，即可得到结论
试题解析：(1)将圆的方程整理为(x2＋y2－20)＋a(－4x＋2y＋20)＝0，…………3分
令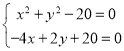
可得
所以该圆恒过定点(4，－2)．…………6分
(2)圆的方程可化为(x－2a)2＋(y＋a)2＝5a2－20a＋20＝5(a－2)2，
所以圆心为(2a，a)，半径为
|a－2|. …………8分
∵两圆外切， ∴
＝2＋
|a－2|，
即
|a|＝2＋
|a－2|，…………10分
由此解得a＝1＋
.
∴ 两圆外切时a＝1＋
…………12分
练习册系列答案
相关题目
