题目内容
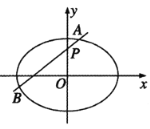
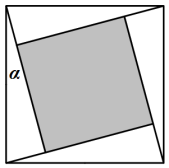
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”，国时期吴国的数学家赵爽创制了一幅“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明
如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个大正方形若直角三角形中较小的锐角
，现在向该大止方形区域内随机地投掷一枚飞镖，则飞镖落在阴影部分的概率是
A. 
B. 
C. 
D. 
【答案】A
【解析】
由解三角形得：直角三角形中较小的直角边长为1，由
，得此直角三角形另外两直角边长为
，进而得小正方形的边长和大正方形的边长，由几何概型中的面积型得解．
设直角三角形中较小的直角边长为1，则由直角三角形中较小的锐角，
得此直角三角形另外直角边长为
，斜边长
，
则小正方形的边长为
，大正方形的边长为，
设“飞镖落在阴影部分”为事件A，
由几何概型中的面积型可得：
，
故选：A．
【题目】“网购”已经成为我们日常生活中的一部分，某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额，数据整理如下：
男性消费金额频数分布表
消费金额 （单位：元） | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
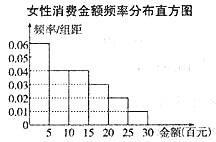
（1）试分别计算男性、女性在此活动中的平均消费金额；
（2）如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费，试问是否有5成以上的把握认为理性消费与性别有关.
附：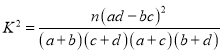
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
【题目】在创建“全国卫生文明城”的过程中，环保部门对某市市民进行了一次垃圾分类知识的网络问卷调查，每一位市民仅有一次参加机会，通过随机抽样，得到参加问卷调查的1000人的得分（满分：100分）数据，统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
（Ⅰ）已知此次问卷调查的得分
服从正态分布
，
近似为这1000人得分的平均值（同一组中的数据用该组区间的中点值为代表），请利用正态分布的知识求
；
（Ⅱ）在（Ⅰ）的条件下，环保部门为此次参加问卷调查的市民制定如下奖励方案：
（i）得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费；
（ii）每次赠送的随机话费和相应的概率如下表.现市民甲要参加此次问卷调查，记
为该市民参加问卷调查获赠的话费，求的分布列及数学期望.
赠送的随机话费（单位：元） | 20 | 40 |
概率 |
|
|
附：若
，则
，
，
.
