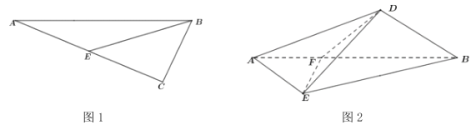
题目内容
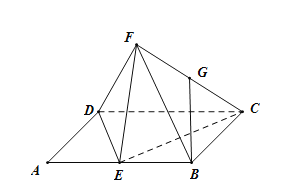
【题目】图1,在![]() 中,
中,![]() ,
,![]() ,E为
,E为![]() 中点.以
中点.以![]() 为折痕将
为折痕将![]() 折起,使点C到达点D的位置,且
折起,使点C到达点D的位置,且![]() 为直二面角,F是线段
为直二面角,F是线段![]() 上靠近A的三等分点,连结
上靠近A的三等分点,连结![]() ,
,![]() ,
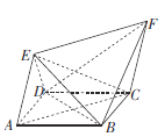
,![]() ,如图2.
,如图2.
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取![]() 中点为M,连结
中点为M,连结![]() ,可得到
,可得到![]() 平面
平面![]() ,所以
,所以![]() .计算
.计算![]() ,
,![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,故可证
,故可证![]() 平面
平面![]() ,从而得到
,从而得到![]() .
.
(2)过E作![]() ,以E为坐标原点,以
,以E为坐标原点,以![]() ,
,![]() ,
,![]() 的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系
的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系![]() ,计算平面
,计算平面![]() 的法向量和直线
的法向量和直线![]() 的方向向量,代入公式计算即可.
的方向向量,代入公式计算即可.
(1)设![]() 中点为M,连结
中点为M,连结![]() .
.
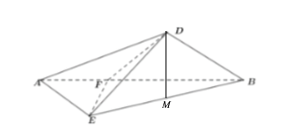
因为E是![]() 中点,所以
中点,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() .
.
因为![]() 为直二面角,即平面
为直二面角,即平面![]() 平面
平面![]() ,
,
又因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,且
,且![]() .
.
因为F是![]() 上靠近A的三等分点,所以
上靠近A的三等分点,所以![]() ,
,![]() .
.
在![]() 中,根据余弦定理,
中,根据余弦定理,![]() ,
,
即![]() ,.
,.
在![]() 中,
中,![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)如图,过E作![]() ,则
,则![]() 平面
平面![]() .
.
以E为坐标原点,以![]() ,
,![]() ,
,![]() 的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系
的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系![]()
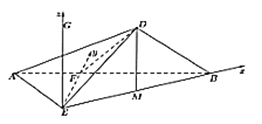
则![]() ,
,![]() ,
,![]() ,
,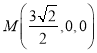 ,
,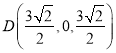 .
.
故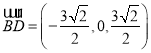 ,
,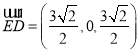 ,
,
![]() ,
,![]() ,
,
那么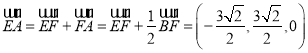 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
则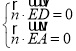 ,即
,即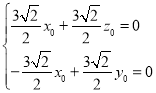 ,
,
取![]() ,得
,得![]() ,
,![]() ,此时
,此时![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则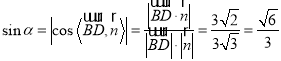 ,
,
即直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目