题目内容
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
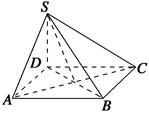

| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
D
选项A正确,因为SD垂直于底面ABCD,而AC?平面ABCD,所以AC⊥SD;再由四边形ABCD为正方形,所以AC⊥BD;而BD与SD相交,所以,AC⊥平面SBD,AC⊥SB.
选项B正确,因为AB∥CD,而CD?平面SCD,AB?平面SCD,所以AB∥平面SCD.
选项C正确,设AC与BD的交点为O,易知SA与平面SBD所成的角就是∠ASO,SC与平面SBD所成的角就是∠CSO,易知这两个角相等.
选项D错误,AB与SC所成的角等于∠SCD,而DC与SA所成的角是∠SAB,这两个角不相等.
选项B正确,因为AB∥CD,而CD?平面SCD,AB?平面SCD,所以AB∥平面SCD.
选项C正确,设AC与BD的交点为O,易知SA与平面SBD所成的角就是∠ASO,SC与平面SBD所成的角就是∠CSO,易知这两个角相等.
选项D错误,AB与SC所成的角等于∠SCD,而DC与SA所成的角是∠SAB,这两个角不相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
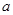 的等边三角形
的等边三角形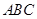 的中线
的中线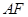 与中位线
与中位线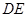 交于点
交于点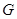 ,已知
,已知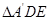 (
(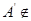 平面
平面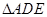 绕
绕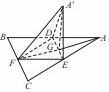
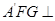 平面
平面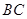 //平面
//平面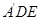 ;
;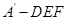 的体积最大值为
的体积最大值为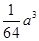 ;
;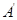 在平面
在平面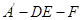 大小的范围是
大小的范围是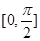 .
.