题目内容
判断下列各函数的奇偶性:
(1)f(x)=(x-2)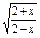 ;
;
(2)f(x)=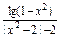 ;
;
(3)f(x)=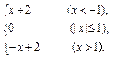
(1)f(x)=(x-2)
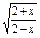 ;
;(2)f(x)=
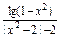 ;
;(3)f(x)=
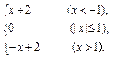
(1)f(x)为非奇非偶函数(2)f(x)为偶函数(3)f(x)是偶函数
(1)由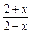 ≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
(2)由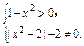 得定义域为(-1,0)∪(0,1).
得定义域为(-1,0)∪(0,1).
这时f(x)=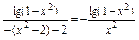 .
.
∵f(-x)=-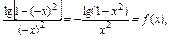 ∴f(x)为偶函数.
∴f(x)为偶函数.
(3)x<-1时,f(x)=x+2,-x>1,
∴f(-x)=-(-x)+2=x+2=f(x).
x>1时,f(x)=-x+2,
-x<-1,f(-x)=x+2=f(x).
-1≤x≤1时,f(x)=0,-1≤-x≤1,
f(-x)=0=f(x).
∴对定义域内的每个x都有f(-x)=f(x).因此f(x)是偶函数.
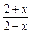 ≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.(2)由
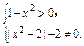 得定义域为(-1,0)∪(0,1).
得定义域为(-1,0)∪(0,1).这时f(x)=
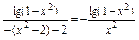 .
.∵f(-x)=-
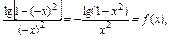 ∴f(x)为偶函数.
∴f(x)为偶函数.(3)x<-1时,f(x)=x+2,-x>1,
∴f(-x)=-(-x)+2=x+2=f(x).
x>1时,f(x)=-x+2,
-x<-1,f(-x)=x+2=f(x).
-1≤x≤1时,f(x)=0,-1≤-x≤1,
f(-x)=0=f(x).
∴对定义域内的每个x都有f(-x)=f(x).因此f(x)是偶函数.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
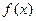 是定义在
是定义在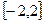 上的奇函数,当
上的奇函数,当 时,
时,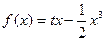 (
(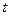 为常数)。
为常数)。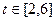 时,求
时,求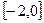 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的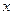 ,并猜想
,并猜想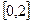 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);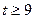 时,证明:函数
时,证明:函数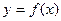 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线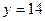 上。
上。





 恰有一个零点,求
恰有一个零点,求 的值
的值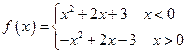 ,判断
,判断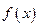 的奇偶性,并加以证明.
的奇偶性,并加以证明.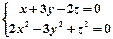 ,则方程组的解(x,y,z)= 。
,则方程组的解(x,y,z)= 。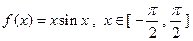 ,若
,若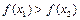 ,则下列不等式必定成立的是
,则下列不等式必定成立的是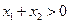
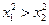
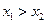
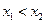
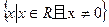 又f(x)在
又f(x)在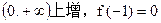 ,则f(x)>0的解集是( )
,则f(x)>0的解集是( )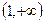 B (0,1) C
B (0,1) C 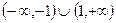 D
D 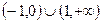
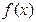 在
在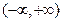 上满足
上满足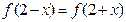 ,
,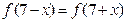 ,则函数
,则函数 为偶函数,则
为偶函数,则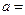 .
.