题目内容
已知函数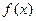 是定义在
是定义在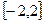 上的奇函数,当
上的奇函数,当 时,
时,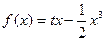 (
(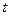 为常数)。
为常数)。
(1)求函数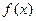 的解析式;
的解析式;
(2)当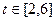 时,求
时,求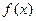 在
在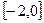 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的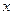 ,并猜想
,并猜想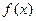 在
在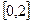 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当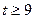 时,证明:函数
时,证明:函数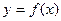 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线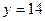 上。
上。
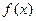 是定义在
是定义在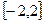 上的奇函数,当
上的奇函数,当 时,
时,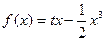 (
(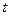 为常数)。
为常数)。(1)求函数
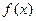 的解析式;
的解析式;(2)当
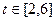 时,求
时,求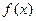 在
在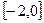 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的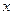 ,并猜想
,并猜想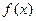 在
在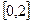 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);(3)当
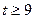 时,证明:函数
时,证明:函数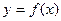 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线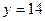 上。
上。(1)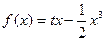 (2)增区间为
(2)增区间为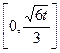 (3)见解析
(3)见解析
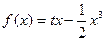 (2)增区间为
(2)增区间为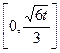 (3)见解析
(3)见解析(1)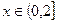 时,
时,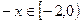 , 则
, 则 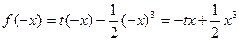 , ∵函数
, ∵函数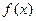 是定义在
是定义在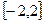 上的奇函数,即
上的奇函数,即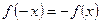 ,∴
,∴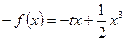 ,
,
即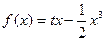 ,又可知
,又可知 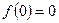 ,∴函数
,∴函数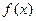 的解析式为
的解析式为 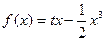 ,
,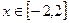 ;
;
(2)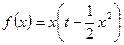 ,∵
,∵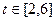 ,
,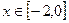 ,∴
,∴ ,
,
∵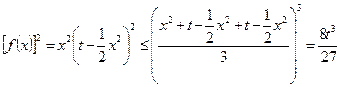 ,∴
,∴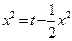 ,
,
即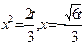
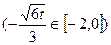 时,
时,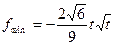 。
。
猜想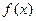 在
在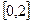 上的单调递增区间为
上的单调递增区间为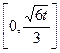 。
。
(3)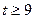 时,任取
时,任取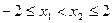 ,
,
∵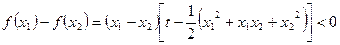 , ∴
, ∴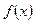 在
在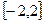 上单调递增,即
上单调递增,即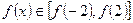 ,即
,即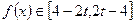 ,
,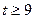 ,
,
∴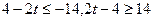 ,∴
,∴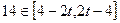 ,∴当
,∴当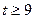 时,函数
时,函数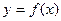 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线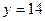 上。
上。
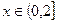 时,
时,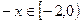 , 则
, 则 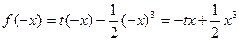 , ∵函数
, ∵函数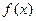 是定义在
是定义在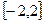 上的奇函数,即
上的奇函数,即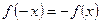 ,∴
,∴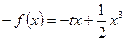 ,
,即
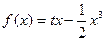 ,又可知
,又可知 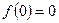 ,∴函数
,∴函数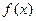 的解析式为
的解析式为 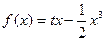 ,
,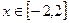 ;
;(2)
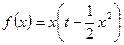 ,∵
,∵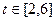 ,
,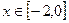 ,∴
,∴ ,
,∵
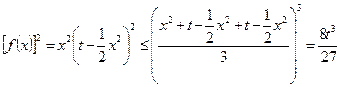 ,∴
,∴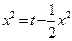 ,
,即
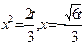
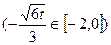 时,
时,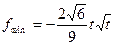 。
。猜想
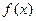 在
在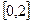 上的单调递增区间为
上的单调递增区间为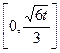 。
。(3)
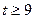 时,任取
时,任取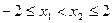 ,
,∵
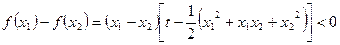 , ∴
, ∴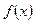 在
在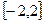 上单调递增,即
上单调递增,即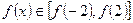 ,即
,即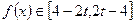 ,
,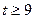 ,
,∴
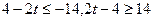 ,∴
,∴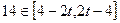 ,∴当
,∴当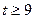 时,函数
时,函数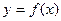 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线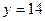 上。
上。
练习册系列答案
相关题目
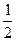 )]<0的解集。
)]<0的解集。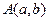 ,
,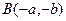 在函数
在函数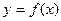 的图像上,称
的图像上,称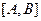 为函数
为函数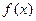 的一组关于原点的中心对称点,
的一组关于原点的中心对称点,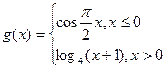 关于原点的中心对称点有多少组
关于原点的中心对称点有多少组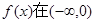 上单调递增,若
上单调递增,若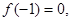 则不等式
则不等式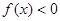 的解集是( )
的解集是( )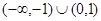
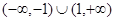
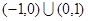
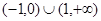
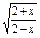 ;
;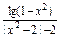 ;
;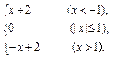
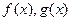 分别是
分别是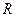 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足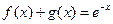 ,则有
,则有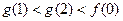
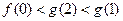
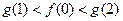
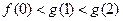
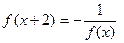 ,
,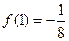 ,
,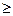 0),则
0),则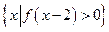 =
=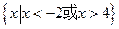
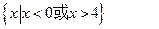
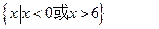
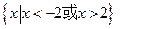
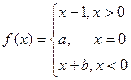 是奇函数,则
是奇函数,则