题目内容
已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.
(1)a="12" b=﹣3 (2)f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);
(3)(﹣∞,﹣1]∪
解析试题分析: (1)由极值的定义和已知条件可得b﹣c=﹣3﹣c,,即b=-3;对已知函数求导,再由 ,列出管a,b 的等式,即可得到a的值.(2)由(1)可得到f(x)的表达式,然后对其求导,由
,列出管a,b 的等式,即可得到a的值.(2)由(1)可得到f(x)的表达式,然后对其求导,由 或
或 ,可得到函数的单调增区间或减区间.(3)求出f(x)的最小值﹣3﹣c,已知条件式f(x)≥﹣2c2恒成立可转化为﹣3﹣c≥﹣2c2,解得c即可.
,可得到函数的单调增区间或减区间.(3)求出f(x)的最小值﹣3﹣c,已知条件式f(x)≥﹣2c2恒成立可转化为﹣3﹣c≥﹣2c2,解得c即可.
试题解析:解:(1)由题意知f(1)=﹣3﹣c,因此b﹣c=﹣3﹣c,从而b=﹣3。2分
又对f(x)求导得 =x3(4alnx+a+4b),
=x3(4alnx+a+4b),
由题意f'(1)=0,因此a+4b=0,得a=12 4分
(2)由(1)知f'(x)=48x3lnx(x>0),令f'(x)=0,解得x=1
当0<x<1时,f'(x)<0, f(x)单调递减;当x>1时,f'(x)>0, f(x)单调递增,
故 f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞) 8分
(3)由(2)知,f(x)在x=1处取得极小值f(1)=﹣3﹣c,此极小值也是最小值,
要使f(x)≥﹣2c2(x>0)恒成立,只需﹣3﹣c≥﹣2c2 10分
即2c2﹣c﹣3≥0,从而(2c﹣3)(c+1)≥0,解得 或c≤﹣1
或c≤﹣1
所以c的取值范围为(﹣∞,﹣1]∪ 12分
12分
考点:1.函数的导数;2.单数的性质;3.不等式恒成立.

 .
.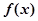 在区间
在区间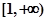 单调递增,求
单调递增,求 的最小值;
的最小值;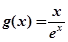 ,对
,对 ,使
,使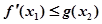 成立,求
成立,求 的范围.
的范围.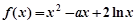 (其中
(其中 是实数).
是实数).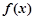 的单调区间;
的单调区间; ,且
,且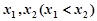 ,求
,求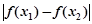 的取值范围.
的取值范围.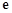 是自然对数的底数)
是自然对数的底数)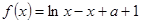
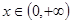 使得
使得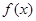 ≥0成立,求
≥0成立,求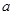 的范围
的范围  >1时,在(1)的条件下,
>1时,在(1)的条件下,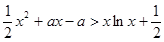 成立
成立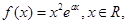 其中
其中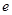 为自然对数的底数,
为自然对数的底数, 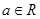 .
.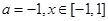 ,求函数
,求函数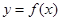 的最值;
的最值;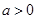 ,都有
,都有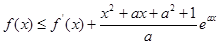 成立,求
成立,求 的取值范围.
的取值范围.
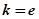 ,试确定函数
,试确定函数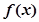 的单调区间;
的单调区间;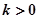 且对任意
且对任意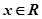 ,
,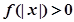 恒成立,试确定实数
恒成立,试确定实数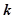 的取值范围;
的取值范围;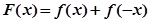 ,求证:
,求证: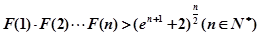
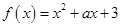 .
.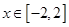 时,
时,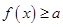 恒成立,求实数
恒成立,求实数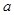 的取值范围;
的取值范围;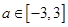 ,
,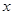 的取值范围.
的取值范围.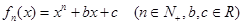
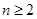 ,
,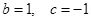 ,证明:
,证明: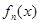 在区间
在区间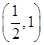 内存在唯一的零点;
内存在唯一的零点;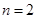 ,若对任意
,若对任意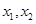
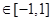 ,有
,有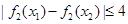 ,求
,求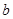 的取值范围
的取值范围 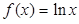 .
.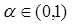 ,求
,求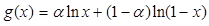 最大值;
最大值;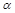 ,
,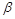 满足
满足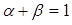 .求证:
.求证: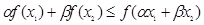 ;
;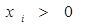 ,正数
,正数 满足
满足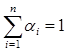 .证明:
.证明: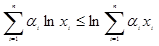
 .
.