题目内容
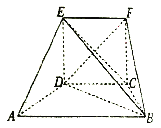
【题目】如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)要证线线垂直,一般是用线面垂直的性质定理,先证线面垂直,本题从图中看,想象能不能证明![]() ,为此要证
,为此要证![]() ,对
,对![]() ,因为
,因为![]() 是
是![]() 在平面
在平面![]() 上的射影,且
上的射影,且![]() ,从而有
,从而有![]() ,对
,对![]() ,可通过求出
,可通过求出![]() 的三边长,由勾股定理得结论;当然结合第(2)小题求二面角,我们还可以以A为坐标原点,过点A垂直于AC的直线为x轴,AC、AE所在的直线分别为y、z轴建立空间直角坐标系.通过向量法证明线线垂直,(2)通过二面角的两个面的法向量来求得二面角.
的三边长,由勾股定理得结论;当然结合第(2)小题求二面角,我们还可以以A为坐标原点,过点A垂直于AC的直线为x轴,AC、AE所在的直线分别为y、z轴建立空间直角坐标系.通过向量法证明线线垂直,(2)通过二面角的两个面的法向量来求得二面角.
试题解析:(1)证法一:![]() ,
,![]() ,又∵BM⊥AC,
,又∵BM⊥AC,![]()
![]() ①
①
而![]()
![]() ,
,![]() ,
,
即![]()
∴![]() ②
②![]() ③
③
由①②③得![]() ,∴EM⊥BF
,∴EM⊥BF
证法二:在Rt△ABC中,AC=4,∠BAC=30°
∴AB=2![]() ,BC=2,又BM⊥AC
,BC=2,又BM⊥AC
则AM=3,BM=![]() .
.
如图,以A为坐标原点,过点A垂直于AC的直线为x轴,AC、AE所在的直线分别为y、z轴
建立空间直角坐标系.
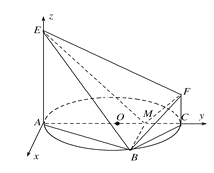
由已知条件得A(0,0,0),M(0,3,0),E(0,0,3),B(![]() ,3,0),F(0,4,1),
,3,0),F(0,4,1),
∴![]() =(0,-3,3),
=(0,-3,3),![]() =(-
=(-![]() ,1,1).
,1,1).
由![]() ·
·![]() =(0,-3,3)·(-
=(0,-3,3)·(-![]() ,1,1)=0,
,1,1)=0,
得![]() ⊥
⊥![]() ,∴EM⊥BF.
,∴EM⊥BF.
(2)解:由(1)知![]() =(-
=(-![]() ,-3,3),
,-3,3),![]() =(-
=(-![]() ,1,1).
,1,1).
设平面BEF的法向量为n=(x,y,z),
由n·![]() =0,n·
=0,n·![]() =0,得
=0,得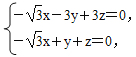
令x=![]() 得y=1,z=2,∴n=(
得y=1,z=2,∴n=(![]() ,1,2),
,1,2),
由已知EA⊥平面ABC,
所以取面ABC的法向量为![]() =(0,0,3),
=(0,0,3),
设平面BEF与平面ABC所成的锐二面角为θ,
则![]() ,
,
平面BEF与平面ABC所成的锐二面角的余弦值为![]() .
.

【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() (Air Pollution Index)的监测数据,结果统计如下:
(Air Pollution Index)的监测数据,结果统计如下:
|
|
|
|
|
|
| 大于300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天数 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
(Ⅰ)若本次抽取的样本数据有30天是在供暖季,其中有7天为重度污染,完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 5.024 | 6.635 | 7.879 | 10.828 |
附: 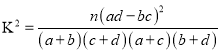
(Ⅱ)政府要治理污染,决定对某些企业生产进行管控,当![]() 在区间
在区间![]() 时企业正常生产;当
时企业正常生产;当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() (即关闭
(即关闭![]() 的产能),当
的产能),当![]() 在区间
在区间![]() 时对企业限产
时对企业限产![]() ,当
,当![]() 在300以上时对企业限产
在300以上时对企业限产![]() ,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
①在这一年中随意抽取5天,求5天中企业被限产达到或超过![]() 的恰为2天的概率;
的恰为2天的概率;
②求企业甲这一年因限产减少的利润的期望值.