题目内容

8．已知f1（x）=sinx+cosx，f n+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，f n+1（x）=fn′（x），n∈N*，则f1（x）+f2（x）+…+f 2011（x）=（　　）
A．-sinx+cosxB．sinx-cosxC．-sinx-cosxD．sinx+cosx

分析 根据题意和求导公式依次求出f2（x）、f3（x）、f4（x）、f 5（x），求出函数的周期，利用周期性求出式子的和．

解答 解：由题意得，f1（x）=sinx+cosx，
∴f2（x）=f1′（x）=cosx-sinx，f3（x）=f2′（x）=-sinx-cosx，
f4（x）=f3′（x）=-cosx+sinx，f5（x）=f4′（x）=sinx+cosx，…，
∴fn（x）的周期是4，且f1（x）+f2（x）+f3（x）+f 4（x）=0，
f1（x）+f2（x）+…+f 2011（x）=502[f1（x）+f2（x）+f3（x）+f 4（x）]+f1（x）+f2（x）+f3（x）
=（sinx+cosx）+（-sinx+cosx）+（-sinx-cosx）=-sinx+cosx，
故选：A．

点评 本题考查求导公式和法则，以及函数周期性的应用，属于基础题．

练习册系列答案
相关题目
18．已知数列{xn}的首项x1，通项公式xn=2np+np（n∈N+，p，q为常数），且x1，x4，x5成等差数列，求：
（1）p，q的值；
（2）数列{xn}的前n项的和Sn的公式．
19．因指数函数y=ax是增函数（大前提），而y=（$\frac{1}{3}$）x是指数函数（小前提），所以y=（$\frac{1}{3}$）x是增函数（结论），上面推理错误的原因是大前提是错误的（填大前提或小前提或结论）．
16．如图在Rt△ABC中∠ACB=90°，CD⊥AB，AC=6，AD=3.6，则BD=6.4．
3．求下列各题中的函数f（x）的解析式．
（1）已知f（$\sqrt{x}+2$）=x+4$\sqrt{x}$，求f（x）
（2）已知函数t=f（x）满足2f（x）+f（$\frac{1}{x}$）=2x，x∈R且x≠0，求f（x）
13．已知离散型随机变量X的分布列为P（X=1）=$\frac{3}{5}$，P（X=2）=$\frac{3}{10}$，P（X=3）=$\frac{1}{10}$，则X的数学期望E（X）=（　　）
A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．3
20．一个几何体的三视图如图所示，则该几何体的体积为（　　）
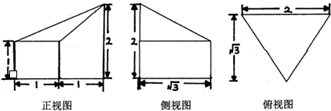
A．$\sqrt{3}$B．2C．$\frac{4\sqrt{3}}{3}$D．2$\sqrt{3}$
17．已知函数f（x）=2x-$\frac{a}{x}$的定义域为（0，1]（其中a是实数）
（1）当a=-1时，求函数y=f（x）的值域；
（2）若函数y=f（x）在定义域上是减函数，求实数a的取值范围；
（3）求不等式f（x）≥0的解集．
18．已知各项均为正数的两个数列{an}和{bn}满足：an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}}$，bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$，n∈N*，
（1）求证：数列{（$\frac{{b}_{n}}{{a}_{n}}$）2}是等差数列；
（2）若a1=b1=1，令（$\frac{{b}_{n}}{{a}_{n}}$）2=$\frac{1}{{c}_{n}}$，求证：$\frac{1}{{{c}_{1}}^{2}}$+$\frac{1}{{{c}_{2}}^{2}}$+$\frac{1}{{{c}_{3}}^{2}}$+…+$\frac{1}{{{c}_{n}}^{2}}$＜2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网