题目内容
5.在所有两位数(10~99)中,任取一个数,能被2或3整除的概率是( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
分析 在所有的两位数(10-99)共有90个,求得其中被2整除的有45个,被3整除的有30个,被6整除的有15个,可得能被2或3整除的数有60个,由此求得这个数能被2或3整除的概率
解答 解:在所有的两位数(10-99)共有90个,其中被2整除的有10,12,14,…,98,共计45个.
被3整除的有12,15,18,…,99,共计30个,
被6整除的有12,18,24,…,96,共计15个,
故能被2或3整除的数有45+30-15=60个.
任取一个数,则这个数能被2或3整除的概率为P=$\frac{60}{90}$=$\frac{2}{3}$.
故选:C.
点评 本题考查古典概型及其概率计算公式的应用,等差数列的通项公式,求得被2或3整除的数有60个,是解题的关键,属于基础题.

练习册系列答案
相关题目
15.因为对数函数y=logax是增函数(大前提),而是对数函数$y={log_{\frac{1}{3}}}x$(小前提),所以y=log${\;}_{\frac{1}{3}}$x是增函数(结论).这个推理过程中( )
| A. | 大前提错误导致结论错误 | |
| B. | 小前提错误导致结论错误 | |
| C. | 推理形式错误导致结论错误 | |
| D. | 大前提和小前提都错误导致结论错误 |
13.已知离散型随机变量X的分布列为P(X=1)=$\frac{3}{5}$,P(X=2)=$\frac{3}{10}$,P(X=3)=$\frac{1}{10}$,则X的数学期望E(X)=( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
20.一个几何体的三视图如图所示,则该几何体的体积为( )
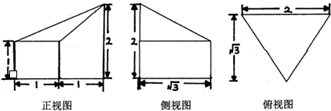

| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
