题目内容
20.某中学举行了一次“环保知识竞赛”.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分100分)作为样本(样本容量为疗)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
(Ⅰ)求样本容量月和频率分布直方图中x,y的值;
(Ⅱ)把在[60,70),[70,80),[80,90)的成绩分组的学生按分层抽样的方法抽取8人.求[60,70),[70,80),[80,90)成绩分组中各应该抽取的人数;
(Ⅲ)在(II)中的8人中随机抽取4名同学到市政广场参加环保知识宣传的志愿者活动,记X为成绩在[60,70)的人数,求X的分布列和数学期望.
分析 (Ⅰ)由样本容量和频数频率的关系能求出样本容量n和频率分布直方图中的x、y的值.
(Ⅱ)利用分层抽样,可得分组中各应该抽取的人数;
(Ⅲ)由题意可知,X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列及数学期望.
解答 解:(Ⅰ)由题意可知,样本容量n=$\frac{8}{0.016×10}$=50,y=$\frac{2}{50×10}$=0.004,
x=0.1-0.004-0.010-0.016-0.04=0.030…(3分)
(Ⅱ)在[60,70),[70,80),[80,90)成绩分组的学生分别为15人,20人,5人,
现要按分层抽样抽取8人,则在[60,70),[70,80),[80,90)成绩分组中各抽取3人,4人,1人…(6分)
(Ⅲ)X=0,1,2,3
P(X=0)=$\frac{{C}_{5}^{4}}{{C}_{8}^{4}}$=$\frac{1}{14}$,P(X=1)=$\frac{{C}_{5}^{3}{C}_{3}^{1}}{{C}_{8}^{4}}$=$\frac{3}{7}$,P(X=2)=$\frac{{C}_{5}^{2}{C}_{3}^{2}}{{C}_{8}^{4}}$=$\frac{3}{7}$,P(X=3)=$\frac{{C}_{5}^{1}{C}_{3}^{3}}{{C}_{8}^{4}}$=$\frac{1}{14}$.
X的分布列为:
| X | 0 | 1 | 2 | 3 |
P | $\frac{1}{14}$ | $\frac{3}{7}$ | $\frac{3}{7}$ | $\frac{1}{14}$ |
∴EX=0×$\frac{1}{14}$+1×$\frac{3}{7}$+2×$\frac{3}{7}$+3×$\frac{1}{14}$=$\frac{3}{2}$…(12分)
点评 本题考查频率分布直方图的应用,考查随机变量X的分布列及数学期望的求法,是中档题.

练习册系列答案
相关题目
10.将甲、乙等5名交警分配到三个不同路口疏导交通,每个路口至少一人,且甲、乙在同一路口的分配方案共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 72种 |
11.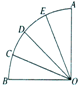 扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )
扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )
 扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )
扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
8.下列结论中,正确的是( )
| A. | 0•$\overrightarrow{a}$=0 | B. | λμ<0,$\overrightarrow{a}≠0$时,λ$\overrightarrow{a}$与μ$\overrightarrow{a}$方向一定相反 | ||
| C. | 若$\overrightarrow{b}$=λ$\overrightarrow{a}$($\overrightarrow{a}≠0$),则$\frac{\overrightarrow{b}}{\overrightarrow{a}}$=λ | D. | 若|$\overrightarrow{b}$|=|λ$\overrightarrow{a}$|($\overrightarrow{a}≠0$),则$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$=λ |
 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.