题目内容
9.已知向量$\overrightarrow{m}$=(cos2x,sinx),$\overrightarrow{n}$=(2,2$\sqrt{3}$cosx),设函数g(x)=$\overrightarrow{m}$•$\overrightarrow{n}$,把g(x)的图象上所有的点向右平移$\frac{5π}{12}$个单位,再向下平移1个单位,得到函数f(x)的图象.(1)求函数f(x)的解析式;
(2)在△ABC中,∠A、∠B、∠C对应的边分别是a、b、c,已知函数f(x)最小正零点为A,△ABC的面积S=5$\sqrt{3}$,b=5,求边长a的值.
分析 (1)首先通过三角函数的恒等变换,把函数的关系式变性成正弦型函数,进一步通过三角函数的图象变换得出结果.
(2)利用上步求出的函数的关系式,进一步利用函数的零点求出A的值,进一步利用三角形的面积和余弦定理求出结果.
解答 解:(1)已知向量$\overrightarrow{m}$=(cos2x,sinx),$\overrightarrow{n}$=(2,2$\sqrt{3}$cosx),设函数g(x)=$\overrightarrow{m}$•$\overrightarrow{n}$,
则:g(x)=$2{cos}^{2}x+2\sqrt{3}sinxcosx$
=$\sqrt{3}sin2x+cos2x+1$
=$2sin(2x+\frac{π}{6})+1$
所以:把g(x)的图象上所有的点向右平移$\frac{5π}{12}$个单位,再向下平移1个单位,
得到函数f(x)=$2sin[2(x-\frac{5}{12}π)+\frac{π}{6}]+1-1$
=2$sin(2x-\frac{2}{3}π)$
(2)在△ABC中,∠A、∠B、∠C对应的边分别是a、b、c,已知函数f(x)最小正零点为A,
则:$f(A)=2sin(2A-\frac{2}{3}π)=0$
由于:0<A<π,
解得:A=$\frac{π}{3}$.
由于△ABC的面积S=5$\sqrt{3}$,b=5
所以:S=$\frac{1}{2}bcsinA=5\sqrt{3}$,
解得:c=4.
所以:a2=b2+c2-2bccosA
解得:a=$\sqrt{21}$.
点评 本题考查的知识要点:三角函数关系式的恒等变换,函数的图象的平移变换,正弦型函数的零点的应用,三角形面积及余弦定理的应用.主要考查学生的应用能力.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差x (度) | 10 | 11 | 13 | 12 | 9 |
| 发芽数y(颗) | 15 | 16 | 17 | 14 | 13 |
(1)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程.据气象预报3月6日的昼夜温差为11℃,请预测3月6日浸泡的30颗种子的发芽数.(结果保留整数)
(2)从3月1日至3月5日中任选两天,记种子发芽数超过15颗的天数为X,求X的概率分布列,并求其数学期望和方差.
| A. | {1} | B. | {1,2} | C. | {-3,1,2} | D. | {-3,0,1} |
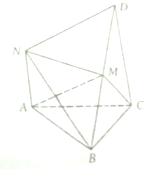 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)