题目内容

10．将甲、乙等5名交警分配到三个不同路口疏导交通，每个路口至少一人，且甲、乙在同一路口的分配方案共有（　　）
A．18种B．24种C．36种D．72种

分析 把甲、乙两名员工看做一个整体，再把这4个人分成3部分，每部分至少一人，共有 ${C}_{4}^{2}$种方法，再把这3部分人分到3个为车间，有${A}_{3}^{3}$种方法，根据分步计数原理，求得不同分法的种数．

解答 解：把甲、乙两名员工看做一个整体，5个人变成了4个，再把这4个人分成3部分，每部分至少一人，
共有 ${C}_{4}^{2}$种方法，
再把这3部分人分到3个为车间，有${A}_{3}^{3}$种方法，
根据分步计数原理，不同分法的种数为${C}_{4}^{2}$•${A}_{3}^{3}$=36，
故选：C．

点评 本题考查的是分类计数问题问题，把计数问题包含在实际问题中，解题的关键是看清题目的实质，把实际问题转化为数学问题，解出结果以后再还原为实际问题，属于基础题．

练习册系列答案
相关题目
3．为了解市民对2015年中央电视台举办的春节联欢晚会的关注情况，某市广电局对该市市民进行了一次随机问卷调查，下面是调查中其中一个方面得到的统计数据．
 看直播 看转播 不看 
男性 480 m 180 
 女性240 150 90 
现按关注方式用分层抽样的方法从参与问卷调查的市民中抽取50名，其中“看直播”的有24名．
（1）求m的值；
（2）该市广电局决定从所调查的“看直播”的720名市民中，仍用分层抽样的方法随机抽取6名进行座谈，再从这6名市民中随机抽取2名颁发幸运礼品，记获得幸运礼品的女性市民的人数为X，求X的分布列及数学期望．
4．化简：（sinα+cosα）2+（sinα-cosα）2．
1．画出下列不等式表示的区域．
（1）（x-y）（x-y-1）≤0；
（2）x≤|y|≤2x．
5．如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（　　）
A．BD∥平面CB1D1
B．AC1⊥B1C
C．AC1⊥平面CB1D1
D．直线CC1与平面CB1D1所成的角为45°
15．（1）f（x）=axex（a≠0），试讨论f（x）的单调性；
（2）求y=x-lnx的单调区间．
2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点A（1，$\frac{\sqrt{3}}{2}$）且离心率为e=$\frac{\sqrt{3}}{2}$．
（1）求椭圆方程；
（2）过点B（-1，0）作直线l，使l与椭圆C交M、N两点，且OM⊥ON，求l的方程．
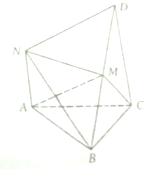19．如图，在几何体NABCD中，CD⊥ABC．DC∥AN，CD=2AN=4，又AB=AC=BC=2，点M是BD上的动点（与B，D不重合）
（1）若M为BD的中点，求证：AM⊥BC；
（2）当直线MN与平面ACDN所成角为30°时，求二面角B-MC-A的正切值．
20．某中学举行了一次“环保知识竞赛”．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分100分）作为样本（样本容量为疗）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．

（Ⅰ）求样本容量月和频率分布直方图中x，y的值；
（Ⅱ）把在[60，70），[70，80），[80，90）的成绩分组的学生按分层抽样的方法抽取8人．求[60，70），[70，80），[80，90）成绩分组中各应该抽取的人数；
（Ⅲ）在（II）中的8人中随机抽取4名同学到市政广场参加环保知识宣传的志愿者活动，记X为成绩在[60，70）的人数，求X的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网