题目内容
已知函数y=f(x)是定义在R上的奇函数,且当x>0时,f(x)+xf′(x)>0(其中f′(x)是f(x)的导函数),设a=(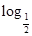 4)f(
4)f(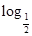 4),b=
4),b=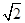 f(
f(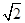 ),c=(lg
),c=(lg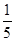 )f(lg
)f(lg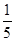 ),则a,b,c由大到小的关系是________.
),则a,b,c由大到小的关系是________.
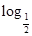 4)f(
4)f(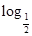 4),b=
4),b=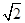 f(
f(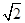 ),c=(lg
),c=(lg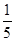 )f(lg
)f(lg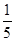 ),则a,b,c由大到小的关系是________.
),则a,b,c由大到小的关系是________.a>b>c
令函数F(x)=xf(x),则函数F(x)=xf(x)为偶函数.当x>0时,F′(x)=f(x)+xf′(x)>0,此时函数F(x)单调递增.则a=F(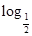 4)=F(-log24)=F(-2)=F(2),b=F(
4)=F(-log24)=F(-2)=F(2),b=F(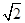 ),c=F(lg
),c=F(lg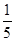 )=F(-lg5)=F(lg5),因为0<lg5<1<
)=F(-lg5)=F(lg5),因为0<lg5<1<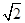 <2,所以a>b>c.
<2,所以a>b>c.
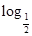 4)=F(-log24)=F(-2)=F(2),b=F(
4)=F(-log24)=F(-2)=F(2),b=F(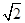 ),c=F(lg
),c=F(lg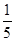 )=F(-lg5)=F(lg5),因为0<lg5<1<
)=F(-lg5)=F(lg5),因为0<lg5<1<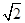 <2,所以a>b>c.
<2,所以a>b>c.
练习册系列答案
相关题目

 的最大值;
的最大值;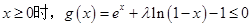 ,求
,求 的取值范围.
的取值范围. +
+
 (n
(n )
)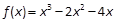 .
.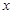 的方程f(x)=a在区间
的方程f(x)=a在区间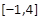 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.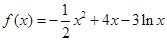 在
在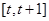 上不单调,则
上不单调,则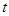 的取值范围是( )
的取值范围是( )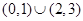
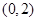
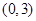
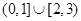
 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围; 是R上的单调函数,则实数m的取值范围是( )。
是R上的单调函数,则实数m的取值范围是( )。


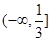

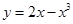 在横坐标为
在横坐标为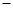 l的点处的切线为
l的点处的切线为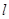 ,则直线
,则直线



 ,若
,若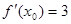 ,则
,则 ( )
( )


