题目内容
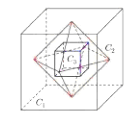
【题目】如图，记棱长为1的正方体
，以各个面的中心为顶点的正八面体为
，以各面的中心为顶点的正方体为
，以各个面的中心为顶点的正八面体为
，……，以此类推得一系列的多面体
，设的棱长为
，则数列
的各项和为________.
【答案】
【解析】
根据条件求出
，
，
，
，然后归纳得到：奇数项与偶数项都是等比数列，然后求和即可.
正方体
各面中心为顶点的凸多面体
为正八面体，
它的中截面（垂直平分对顶点连线的界面）是正方形，
该正方形对角线的长度等于正方体的棱长，
所以
，
以各个面的中心为顶点的凸多面体
为正方体，
正方体面对角线长等于棱长的
，（正三角形中心到对边的距离等于高的），
因此对角线为
，所以
，
以上方式类推得到
，
，
，
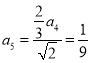所以
各项为
，
奇数项是以
为首项，以
为公比的等比数列，
偶数项是以
为首项，以为公比的等比数列，
所以数列的各项和为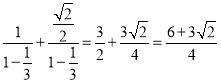
.
故答案为：.
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】某人某天的工作是：驾车从
地出发，到
两地办事，最后返回地，
三地之间各路段行驶时间及当天降水概率如表：
路段 | 正常行驶所需时间（小时） | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水，则在该路段行驶的时间需延长1小时，现有如下两个方案：
方案甲：上午从地出发到
地办事，然后到达
地，下午在地办事后返回地；
方案乙：上午从地出发到地办事，下午从
地出发到达地， 办事后返回地.
（1）设此人8点从地出发，在各地办事及午餐的累积时间为2小时.且采用方案甲，求他当日18点或18点之前能返回地的概率；
（2）甲、乙两个方案中，哪个方案有利于办完事后能更早返回地？
