题目内容
(本小题满分14分)
已知点(1,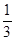 )是函数
)是函数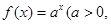 且
且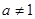 )的图象上一点,等比数列
)的图象上一点,等比数列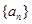 的前
的前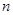 项和为
项和为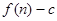 ,数列
,数列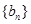
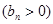 的首项为
的首项为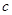 ,且前
,且前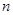 项和
项和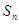 满足
满足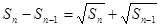 (
(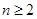 ).
).
(1)求数列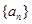 和
和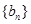 的通项公式;
的通项公式;
(2)若数列{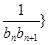 前
前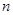 项和为
项和为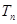 ,问
,问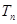 >
>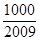 的最小正整数
的最小正整数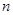 是多少?
是多少?
已知点(1,
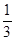 )是函数
)是函数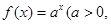 且
且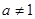 )的图象上一点,等比数列
)的图象上一点,等比数列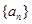 的前
的前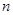 项和为
项和为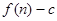 ,数列
,数列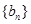
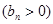 的首项为
的首项为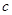 ,且前
,且前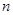 项和
项和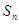 满足
满足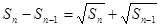 (
(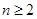 ).
).(1)求数列
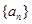 和
和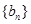 的通项公式;
的通项公式;(2)若数列{
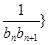 前
前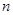 项和为
项和为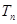 ,问
,问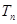 >
>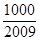 的最小正整数
的最小正整数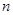 是多少?
是多少? (1)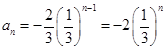 ,
,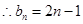
(2) 112
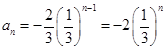 ,
,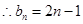
(2) 112
试题分析:(1)依题意
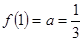 ,
,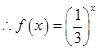 ……………1分
……………1分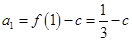 ,
,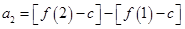
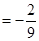 ,
,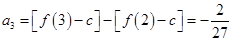 .
.又数列
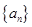 成等比数列,
成等比数列,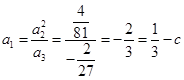 ,所以
,所以 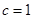 ;……………3分
;……………3分又公比
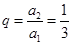 ,所以
,所以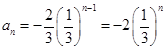
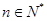 ;……………4分
;……………4分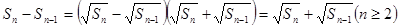
又
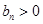 ,
,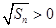 ,
, 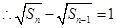 ;
;数列
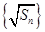 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,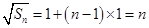 ,
, 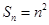 ……………7分
……………7分当
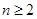 ,
, 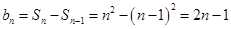 ;当
;当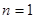 时
时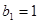 符合上式
符合上式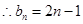 (
(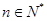 );……………9分
);……………9分(2)
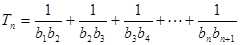
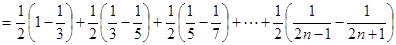
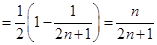 ;……………12分
;……………12分由
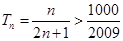 得
得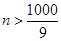 ,满足
,满足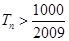 的最小正整数为112.………14分
的最小正整数为112.………14分点评:根据已知的数列的求和与其通项公式的关系式来求解数列的通项公式,并能结合裂项法求和,属于基础题。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
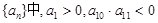 ,若此数列的前10项和
,若此数列的前10项和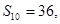 前18项和
前18项和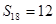 ,则数列
,则数列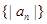 的前18项和
的前18项和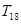 的值是
的值是 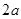 ,1,
,1,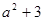 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.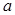 的值;
的值;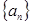 的首项、公差都为
的首项、公差都为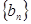 的首项、公比也都为
的首项、公比也都为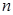 项和分别
项和分别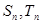 ,且
,且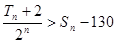 ,求满足条件的正整数
,求满足条件的正整数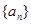 中,
中,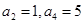 ,则
,则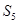 =( )
=( )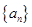 的前
的前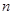 项和是
项和是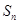 ,若
,若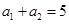 ,
,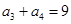 ,则
,则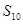 的值为( )
的值为( )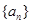 是公比
是公比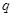 大于1的等比数列,
大于1的等比数列,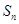 为数列
为数列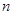 项和,已知
项和,已知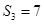 ,且
,且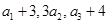 构成等差数列.
构成等差数列.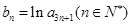 ,求数列
,求数列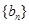 的前
的前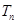 .
.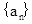 满足:
满足: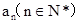 是整数,且
是整数,且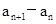 是关于x的方程
是关于x的方程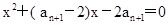 的根.
的根.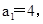 且n≥2时,
且n≥2时,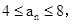 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;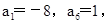 且
且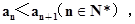 求数列
求数列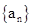 的通项公式.
的通项公式.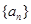 是等差数列,首项公差
是等差数列,首项公差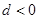 ,
,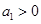 ,且
,且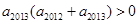 ,则使数列
,则使数列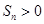 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )