题目内容
【题目】已知直线![]() 经过椭圆E:
经过椭圆E:![]() (
(![]() )的左焦点和下顶点,原点
)的左焦点和下顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.

(1)求椭圆![]() 的离心率;
的离心率;
(2)如上图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)求出经过点![]() 和
和![]() 的直线方程,运用点到直线的距离公式,结合离心率公式即可计算出答案
的直线方程,运用点到直线的距离公式,结合离心率公式即可计算出答案
(2)由(1)知椭圆的方程为![]() ,设出直线AB的方程,代入椭圆方程,运用韦达定理和弦长公式,结合圆的直径和中点坐标公式,解方程即可求出
,设出直线AB的方程,代入椭圆方程,运用韦达定理和弦长公式,结合圆的直径和中点坐标公式,解方程即可求出![]()
解:(1)过点![]() ,
,![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
则原点![]() 到直线的距离
到直线的距离![]() ,
,
得![]() ,
,![]() .
.
(2)由(1)知,椭圆![]() 的方程为
的方程为![]() .
.
依题意,圆心![]() 是线段
是线段![]() 的中点,
的中点,
所以![]() 且
且![]() 不与
不与![]() 轴垂直.
轴垂直.
设其直线方程为![]() ,代入椭圆方程得
,代入椭圆方程得
![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
由![]() ,得
,得![]() ,解得
,解得![]() .从而
.从而![]() .
.
于是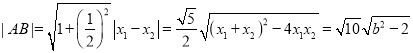 .
.
由![]() ,得
,得![]() ,解得
,解得![]() .故椭圆
.故椭圆![]() 的方程为
的方程为![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】中国农业银行开始为全国农行ATM机安装刷脸取款系统.某农行营业点为调查居民对刷脸取款知识的了解情况,制作了刷脸取款知识有奖调查问卷,发放给2018年度该行的所有客户,并从参与调查且年龄(单位:岁)在[25,55]内的客户中随机抽取100名给予物质奖励,再从中选出一名客户参加幸运大抽奖.调查结果按年龄分成6组,制作成如下的频数分布表和女客户的年龄茎叶图,其中a∶b∶c=2∶4∶5.
年龄/岁 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55] |
频数/人 | 5 | a | b | c | 15 | 25 |
女客户的年龄茎叶图

幸运大抽奖方案如下:客户最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
(1)求a,b,c的值,若分别从男、女客户中随机选取1人,求这2人的年龄均在[40,45)内的概率;
(2)若参加幸运大抽奖的客户所获奖金(单位:元)用X表示,求X的分布列与数学期望E(X).
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
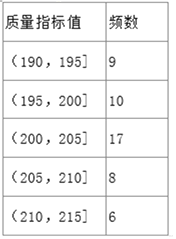
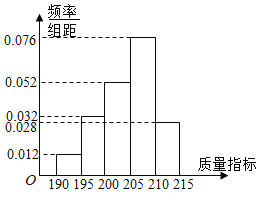
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |