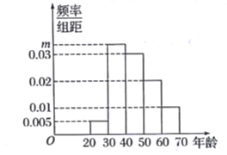
题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆相交另一点
与椭圆相交另一点![]() ,若
,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
【答案】(1)![]() ;(2)
;(2) ![]() 或
或![]()
【解析】
(1)根据离心率![]()
![]() ,和菱形的面积为4,即
,和菱形的面积为4,即![]() 求解。
求解。
(2)由(1)可知点A的坐标是(-2,0).设点B的坐标为![]() ,直线l的斜率为k.则直线l的方程为y=k(x+2).与椭圆方程联立
,直线l的斜率为k.则直线l的方程为y=k(x+2).与椭圆方程联立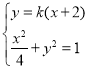 消去y并整理,得
消去y并整理,得![]() .再利用两点间的距离公式,通过
.再利用两点间的距离公式,通过![]() 求解。
求解。
(1)由![]()
![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() .
.
由题意可知![]() ,
,
即![]() .
.
所以![]() .
.
所以椭圆的方程为![]() .
.
(2)由(1)可知点A的坐标是(-2,0)
.设点B的坐标为![]() ,直线l的斜率为k.
,直线l的斜率为k.
则直线l的方程为y=k(x+2).
直线l的方程与椭圆方程联立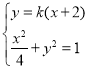 消去y并整理,
消去y并整理,
得![]() .
.
由![]() ,得
,得![]() .从而
.从而![]() .
.
所以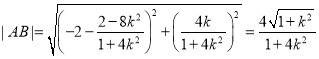 .
.
由![]() ,得
,得![]() .
.
整理得![]() ,
,
即![]() ,解得k=
,解得k=![]() .适合
.适合![]()
所以直线l的倾斜角为![]() 或
或![]() .
.

练习册系列答案
相关题目