题目内容
【题目】中国农业银行开始为全国农行ATM机安装刷脸取款系统.某农行营业点为调查居民对刷脸取款知识的了解情况,制作了刷脸取款知识有奖调查问卷,发放给2018年度该行的所有客户,并从参与调查且年龄(单位:岁)在[25,55]内的客户中随机抽取100名给予物质奖励,再从中选出一名客户参加幸运大抽奖.调查结果按年龄分成6组,制作成如下的频数分布表和女客户的年龄茎叶图,其中a∶b∶c=2∶4∶5.
年龄/岁 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55] |
频数/人 | 5 | a | b | c | 15 | 25 |
女客户的年龄茎叶图

幸运大抽奖方案如下:客户最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.
(1)求a,b,c的值,若分别从男、女客户中随机选取1人,求这2人的年龄均在[40,45)内的概率;
(2)若参加幸运大抽奖的客户所获奖金(单位:元)用X表示,求X的分布列与数学期望E(X).
【答案】(1)![]() ,概率为
,概率为![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据![]() 解方程组,求得
解方程组,求得![]() 的值.先根据茎叶图求得每组内女客户的人数,进而求得每组男客户的人数,然后根据相互独立事件概率计算公式,求得所求的概率.(2)先求得
的值.先根据茎叶图求得每组内女客户的人数,进而求得每组男客户的人数,然后根据相互独立事件概率计算公式,求得所求的概率.(2)先求得![]() 所有可能取值为
所有可能取值为![]() .然后根据分类和分步计算原理求得对应的概率,由此求得分布列和数学期望.
.然后根据分类和分步计算原理求得对应的概率,由此求得分布列和数学期望.
(1)由频数分布表知,a+b+c=100-45=55.
因为a∶b∶c=2∶4∶5,
所以a=![]() ×55=10,b=
×55=10,b=![]() ×55=20,c=
×55=20,c=![]() ×55=25,由茎叶图可知年龄在[25,30)内的女客户有2人,年龄在[30,35)内的女客户有4人,年龄在[35,40)内的女客户有8人,年龄在[40,45)内的女客户有10人,年龄在[45,50)内的女客户有6人,年龄在[50,55]内的女客户有10人,
×55=25,由茎叶图可知年龄在[25,30)内的女客户有2人,年龄在[30,35)内的女客户有4人,年龄在[35,40)内的女客户有8人,年龄在[40,45)内的女客户有10人,年龄在[45,50)内的女客户有6人,年龄在[50,55]内的女客户有10人,
故年龄在[40,45)内的男客户有15人,在100名客户中,男客户有60人,女客户有40人,所以从男客户中随机选取1人,年龄恰在[40,45)内的概率P1=![]() ,
,
从女客户中随机选取1人,年龄恰在[40,45)内的概率P2=![]() ,
,
则分别从男、女客户中随机选取1人,这2人的年龄均在[40,45)内的概率P=P1×P2=![]() .
.
(2)由题意可知,X的所有可能取值为0,5000,10000,则
P(X=0)=![]() ,
,
P(X=5000)=![]() ,
,
P(X=10000)=![]() .
.
X的分布列为
X | 0 | 5 000 | 10 000 |
P |
|
|
|
E(X)=0×![]() +5000×
+5000×![]() +10000×
+10000×![]() =5200(元).
=5200(元).

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 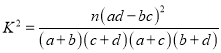 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |