题目内容
15.几何体的三视图如图,则其体积为( )
| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | 2π-1 | D. | 4π-1 |
分析 根据几何体的三视图,得出该几何体是底面半径为1,高为2的圆柱体,
去掉高为1的$\frac{1}{4}$圆柱体所得的几何体;由此求出它的体积.
解答 解:根据几何体的三视图,得,
该几何体是底面半径为1,高为2的圆柱体,
去掉高为1的$\frac{1}{4}$圆柱体所得的几何体;
∴该几何体的体积为
π12×2-$\frac{1}{4}$•π12×1=$\frac{7π}{4}$.
故选:B.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征是什么,是基础题目.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
6.已知双曲线M的焦点与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点相同.如果直线y=-$\sqrt{2}$x是M的一条渐近线,那么M的方程为( )
| A. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{18}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
3.当双曲线C不是等轴双曲线时,我们把以双曲线C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”.则离心率为$\sqrt{3}$的双曲线的“伴生椭圆”的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
7.直线l:y=kx-1与圆x2+y2=1相交于A、B两点,则△OAB的面积最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
4.已知a=0.80.2,b=0.80.5,c=5.20.1,则这三个数的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
5.设全集U=R,已知集合M={x|x2-x>0},N={x|$\frac{x-1}{x}$<0},则有( )
| A. | M∪N=R | B. | M∩N=∅ | C. | CuN=M | D. | CvM⊆N |
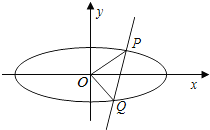 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).