题目内容
【题目】已知椭圆C经过点A(2,3)、B(4,0),对称轴为坐标轴,焦点F1、F2在x轴上.
(1)求椭圆C的方程;
(2)求∠F1AF2的角平分线所在的直线l与椭圆C的另一个交点的坐标.
【答案】
(1)解:∵椭圆C经过点A(2,3)、B(4,0),对称轴为坐标轴,焦点F1、F2在x轴上,
∴设椭圆C的方程为 ![]() =1,a>b>0,
=1,a>b>0,
则 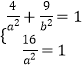 ,解得a2=16,b2=12,
,解得a2=16,b2=12,
∴椭圆C的方程为 ![]() .
.
(2)解:∵椭圆C的方程为 ![]() ,
,
∴F1(﹣2,0),F2(2,0),则直线AF1的方程为y= ![]() ,即3x﹣4y+6=0,
,即3x﹣4y+6=0,
直线AF2的方程为x=2,由点A在椭圆C上的位置得直线l的斜率为正数,
设P(x,y)为直线l上一点,则 ![]() =|x﹣2|,
=|x﹣2|,
解得2x﹣y﹣1=0或x+2y﹣8=0(斜率为负,舍),
∴直线l的方程为2x﹣y﹣x=0,
由 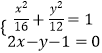 ,整理,得19x2﹣16x﹣44=0,
,整理,得19x2﹣16x﹣44=0,
设直线l与椭圆C的另一个交点为M(x0,y0),
则有 ![]() ,解得
,解得 ![]() ,
, ![]() ,
,
∴直线l与椭圆C的另一个交点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
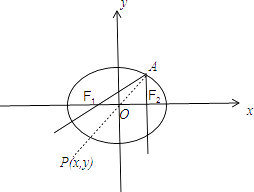
【解析】(1)设椭圆C的方程为 ![]() =1,a>b>0,利用待定系数法能求出椭圆C的方程.(2)直线AF1的方程为3x﹣4y+6=0,求出直线l的方程为2x﹣y﹣x=0,与椭圆联立,得19x2﹣16x﹣44=0,由此利用韦达定理能求出直线l与椭圆C的另一个交点坐标.
=1,a>b>0,利用待定系数法能求出椭圆C的方程.(2)直线AF1的方程为3x﹣4y+6=0,求出直线l的方程为2x﹣y﹣x=0,与椭圆联立,得19x2﹣16x﹣44=0,由此利用韦达定理能求出直线l与椭圆C的另一个交点坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
