题目内容
【题目】已知函数f(x)=sin(ωx+φ)+1(0≤φ≤ ![]() )的图象相邻两对称轴之间的距离为π,且在x=
)的图象相邻两对称轴之间的距离为π,且在x= ![]() 时取得最大值2.
时取得最大值2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当f(α)= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求sinα的值.
,求sinα的值.
【答案】
(1)解:∵若f(x)图象上相邻两条对称轴之间的距离为π,
∴三角函数的周期T=2π,即T= ![]() =2π,即ω=1,
=2π,即ω=1,
则f(x)=sin(x+φ),
当x= ![]() 时,f(x)取得最大值,
时,f(x)取得最大值,
即:sin( ![]() +φ)=1,
+φ)=1,
即: ![]() +φ=
+φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
即:φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
∵|φ|≤ ![]() ,
,
∴φ= ![]() ,
,
则函数f(x)的解析式为:f(x)=sin(x+ ![]() )+1.
)+1.
(2)解:令2kπ﹣ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
解得:2kπ﹣ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,k∈Z,
,k∈Z,
可得函数f(x)的单调递增区间为:[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
(3)解:∵f(α)=sin(α+ ![]() )+1=
)+1= ![]() ,可得:sin(α+
,可得:sin(α+ ![]() )=
)= ![]() ,
,
∵ ![]() <α<
<α< ![]() ,可得:
,可得: ![]() <
< ![]() <π,
<π,
∴cos(α+ ![]() )=﹣
)=﹣ ![]() =﹣
=﹣ ![]() .
.
∴sinα=sin[(α+ ![]() )﹣
)﹣ ![]() ]=sin(α+
]=sin(α+ ![]() )cos
)cos ![]() ﹣cos(α+
﹣cos(α+ ![]() )sin
)sin ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )×
)× ![]() =
= ![]() .
.
【解析】(1)根据三角函数的图象和性质,分别求出周期,利用正弦函数的单调性即可得到结论.(2)令2kπ﹣ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得函数f(x)的单调递增区间.(3)由f(α)=
,k∈Z,即可解得函数f(x)的单调递增区间.(3)由f(α)= ![]() ,可得sin(α+
,可得sin(α+ ![]() )的值,可求范围
)的值,可求范围 ![]() <
< ![]() <π,利用同角三角函数基本关系式可求cos(α+
<π,利用同角三角函数基本关系式可求cos(α+ ![]() )的值,由于α=(α+
)的值,由于α=(α+ ![]() )﹣
)﹣ ![]() ,利用两角差的正弦函数公式即可计算得解.
,利用两角差的正弦函数公式即可计算得解.

【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
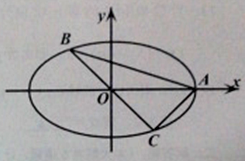
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
【题目】探究函数![]() 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间 上递增.
在区间 上递增.
当![]() 时,
时, ![]() .
.
证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
思考:函数![]() 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)