题目内容
2.已知函数f(x)=ax2+1,g(x)=ln(x+1)(1)实数a为何值时,函数g(x)在x=0处的切线与函数f(x)的图象也相切;
(2)当x∈[0,+∞)时,都有不等式f(x)+g(x)≤x+1成立,求a的取值范围;
(3)已知n∈N,试判断g(n)与g′(1)+g′(2)+…+g′(n-1)的大小,并证明之.
分析 (1)求出函数g(x)的导数,得到方程组,从而求出a的值;
(2)问题转化为:ax2+ln(x+1)-x≤0恒成立,设h(x)=ax2+ln(x+1)-x(x≥0),只需h(x)max≤0即可,求出函数h(x)的导数,讨论a的范围,得到函数h(x)的单调性,从而求出a的范围;
(3)通过ln(x+1)≤x,令x=$\frac{1}{n}$,则ln($\frac{1}{n}$+1)≤$\frac{1}{n}$,继而可得ln(n+1)-lnn<$\frac{1}{n}$,从而证出结论.
解答 解:(1)∵g(x)=ln(x+1),∴g′(x)=$\frac{1}{x+1}$,∴g′(0)=1,
故g(x)在x=0处的切线方程为y=x,
由$\left\{\begin{array}{l}{y=x}\\{y={ax}^{2}+1}\end{array}\right.$,得ax2-x+1=0,
∴1-4a=0,∴a=$\frac{1}{4}$,
(2)当x∈[0,+∞)时,不等式f(x)+g(x)≤x+1成立,
即ax2+ln(x+1)-x≤0恒成立,
设h(x)=ax2+ln(x+1)-x(x≥0),只需h(x)max≤0即可,
由h′(x)=2ax+$\frac{1}{x+1}$-1=$\frac{x[2ax+(2a-1)]}{x+1}$,
①a=0时,h′(x)=-$\frac{x}{x+1}$,
当x>0时,h′(x)<0,
函数h(x)在(0,+∞)上单调递减,
故h(x)≤h(0)=0成立;
②a>0时,由h′(x)=0,解得:x=$\frac{1}{2a}$-1或x=0,
若$\frac{1}{2a}$-1<0,即a>$\frac{1}{2}$时,在区间(0,+∞)上,h′(x)>0,
则函数h(x)在(0,+∞)单调递增,h(x)在[0,+∞)无最大值,不满足条件,
若$\frac{1}{2a}$-1≥0,即0<a≤$\frac{1}{2}$时,
则函数h(x)在(0,$\frac{1}{2a}$-1)单调递减,在($\frac{1}{2a}$-1,+∞)单调递增,
同样,h(x)在[0,+∞)无最大值,不满足条件;
③a<0时,由h′(x)=$\frac{x[2ax+(2a-1)]}{x+1}$,
∵x∈[0,+∞),∴2ax+(2a-1)<0,
∴h′(x)<0,故函数h(x)在[0,+∞)单调递减,故h(x)≤h(0)=0成立,
综上,实数a的范围是[-∞,0];
(3)证明如下:由(2)得,当a=0时,ln(x+1)≤x,
令x=$\frac{1}{n}$,则ln($\frac{1}{n}$+1)≤$\frac{1}{n}$,
∴ln(n+1)-lnn<$\frac{1}{n}$,
故lnn-ln(n-1)<$\frac{1}{n-1}$,
ln(n-1)-ln(n-2)<1$\frac{1}{n-2}$,
…,
ln3-ln2<$\frac{1}{2}$,
ln2-ln1<1,
∴ln(n+1)<1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$,
即g(n)<g′(1)+g′(2)+…+g′(n-1).
点评 本题考察了导数的应用,函数的单调性问题,考察分类讨论思想,本题属于一道难题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
| A. | -1006 | B. | 1007 | C. | -1008 | D. | 1009 |
 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )| A. | $\frac{10}{3}$ | B. | 3 | C. | $\frac{14}{3}$ | D. | 4 |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
 ,那么数列
,那么数列 是( )
是( ) 的图象上存在两点关于
的图象上存在两点关于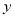 轴对称,则实数
轴对称,则实数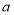 的取值范围是( )
的取值范围是( )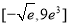 D.
D.
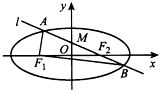 如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.
如图,椭圆C的左、右焦点分别为F1、F2,过F2的直线l交C于A,B两点,△ABF1的周长为8,且F2与抛物线y2=4x的焦点重合.