题目内容
9．已知函数f（x）=x2-4x+3，集合M={（x，y）|f（x）+f（y）≤0}，集合N={（x，y）|f（x）-f（y）≥0}，则集合M∩N面积为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | $\frac{3π}{2}$ |
分析 先分析M，N所表示的平面区域，并在平面直角坐标系中用图形表示出来，最后结合平面几何的知识解决问
解答 解：因为f（x）=x2-4x+3=（x-2）2-1，f（y）=（y-2）2-1，
则f（x）+f（y）=（x-2）2+（y-2）2-2，f（x）-f（y）=（x-2）2-（y-2）2．
∴M={（x，y）=（x-2）2+（y-2）2≤2}，
N={（x，y）||y-2|≤|x-2|}．
故集合M∩N所表示的平面区域为两个扇形，
其面积为圆面积的一半，即为π．
故选：C．
点评 求限制条件（一般用不等式组来表示）所表示平面区域的面积，一般分为如下步骤：①化简不等式②分析不等式表示的平面区域③画出草图分析可行域④结合平面几何知识求出面积
练习册系列答案
名校课堂系列答案
相关题目
18．已知双曲线x2-$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1，F2双曲线的离心率为e，若双曲线上一点P使$\frac{sin∠PF{{\;}_{2}F}_{1}}{sin∠P{F}_{1}{F}_{2}}$=e，Q点为直线PF1上的一点，且$\overrightarrow{PQ}$=3$\overrightarrow{Q{F}_{1}}$，则$\overrightarrow{{F}_{2}Q}$•$\overrightarrow{F{{\;}_{2}F}_{1}}$的值为（ ）
| A． | $\frac{25}{2}$ | B． | $\frac{\sqrt{10}}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
14．某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器，已知他们制作采集器的抛物面的轴切线为经过定点P（1，2）的抛物线，则该抛物线的焦点与双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1在一三象限内的渐近线的距离为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$或$\frac{1}{16}$ | C． | $\frac{1}{16}$ | D． | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
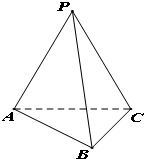如图，在三棱锥P-ABC中，平面APC⊥平面ABC，且PA=PB=PC=4，AB=BC=2．
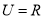，集合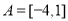
，
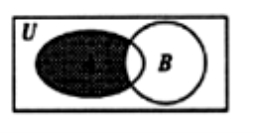
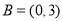，则右图中阴影部分所表示的集合为________.