题目内容
10.已知x、y满足约束条件$\left\{\begin{array}{l}{x+y-4≤0}\\{2x+y-2≥0}\\{3x-y-5≤0}\end{array}\right.$,则z=$\frac{3}{2}$x+3y的最大值为15.分析 画出可行域,利用z为目标函数平移过可行域的A,求出z有最大值.
解答 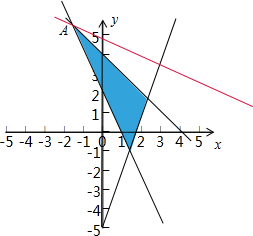 解:画出$\left\{\begin{array}{l}x+y-4≤0\\ 2x+y-2≥0\\ 3x-y-5≤0\end{array}\right.$的可行域如图,平移z=$\frac{3}{2}$x+3y,目标函数经过A时,目标函数取得最大值,由$\left\{\begin{array}{l}x+y-4=0\\ 2x+y-2=0\end{array}\right.$,解得x=-2,y=6,z=$\frac{3}{2}×(-2)+3×6$=15.
解:画出$\left\{\begin{array}{l}x+y-4≤0\\ 2x+y-2≥0\\ 3x-y-5≤0\end{array}\right.$的可行域如图,平移z=$\frac{3}{2}$x+3y,目标函数经过A时,目标函数取得最大值,由$\left\{\begin{array}{l}x+y-4=0\\ 2x+y-2=0\end{array}\right.$,解得x=-2,y=6,z=$\frac{3}{2}×(-2)+3×6$=15.
故答案为:15.
点评 本题考查线性规划问题,考查数形结合,难度较小.

练习册系列答案
相关题目
5.已知向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$=(1,-2)的夹角为π,|$\overrightarrow{AB}$|=2$\sqrt{5}$,点A的坐标为(3,-4).则点B坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (5,-8) | D. | (-8,5) |
15.已知点A(x1,y1),B(x2,y2)是抛物线y2=4x上相异两点,且满足x1+x2=4,若AB的垂直平分线交x轴于点M,则AMB的面积的最大值是( )
| A. | $\frac{16\sqrt{6}}{3}$ | B. | 8 | C. | $\frac{5\sqrt{15}}{3}$ | D. | 6 |
18.已知双曲线x2-$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1,F2双曲线的离心率为e,若双曲线上一点P使$\frac{sin∠PF{{\;}_{2}F}_{1}}{sin∠P{F}_{1}{F}_{2}}$=e,Q点为直线PF1上的一点,且$\overrightarrow{PQ}$=3$\overrightarrow{Q{F}_{1}}$,则$\overrightarrow{{F}_{2}Q}$•$\overrightarrow{F{{\;}_{2}F}_{1}}$的值为( )
| A. | $\frac{25}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
 ,
, ,
, ,
, ,
, ,
, ,…
,… ,1,
,1, ,
, ,…
,…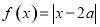 ,
, .
.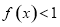 的解集为
的解集为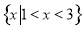 ,求
,求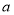 的值;
的值;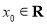 ,使
,使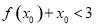 ,求
,求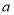 的取值范围.
的取值范围.