Question

11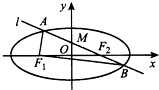．如图，椭圆C的左、右焦点分别为F₁、F₂，过F₂的直线l交C于A，B两点，△ABF₁的周长为8，且F₂与抛物线y²=4x的焦点重合．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l交y轴于点M，且$\overrightarrow{MA}$=λ$\overrightarrow{A{F}_{2}}$，$\overrightarrow{MB}$=μ$\overrightarrow{B{F}_{2}}$，求λ+μ的值；
（Ⅲ）是否存在实数t，使得|AF₂|+|BF₂|=t|AF₂|•|BF₂|恒成立？若存在，求t的值；若不存在，请说明理由．

Answer 1

分析 （I）设椭圆C的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$，抛物线y²=4x的焦点为F₂（1，0），可得c．由△ABF₁的周长为8，可得4a=8，解得a．再利用b²=a²-c²即可得出．
（II）由题意可设直线l的方程为：y=k（x-1），则M（0，-k），设A（x₁，y₁），B（x₂，y₂）．直线方程与椭圆方程联立可得（3+4k²）x²-8k²x+4（k²-3）=0，利用根与系数的关系、向量的坐标运算可得$λ=\frac{{x}_{1}}{1-{x}_{1}}$，μ=$\frac{{x}_{2}}{1-{x}_{2}}$，即可得出λ+μ．
（III）分类讨论：当直线l⊥x轴时，l的方程为：x=1．联立$\left\{\begin{array}{l}{x=1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$，解得A，B．即可得出t=$\frac{4}{3}$．当直线l与x轴不垂直时，设l的方程为：y=k（x-1），不妨设x₂＞1＞x₁，则|AF₂|=$|{x}_{1}-1|•\sqrt{1+{k}^{2}}$，|BF₂|=$|{x}_{2}-1|•\sqrt{1+{k}^{2}}$，x₂-x₁=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$，即可得出$\frac{1}{|A{F}_{2}|}+\frac{1}{|B{F}_{2}|}$=$\frac{4}{3}$．

解答 解：（I）设椭圆C的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$，抛物线y²=4x的焦点为F₂（1，0），∴c=1．
∵△ABF₁的周长为8，∴4a=8，解得a=2．
∴b²=a²-c²=3．
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$．
（II）由题意可设直线l的方程为：y=k（x-1），则M（0，-k），设A（x₁，y₁），B（x₂，y₂）．
联立$\left\{\begin{array}{l}{y=k（x-1）}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$，化为（3+4k²）x²-8k²x+4（k²-3）=0，
则x₁+x₂=$\frac{8{k}^{2}}{3+4{k}^{2}}$，x₁x₂=$\frac{4（{k}^{2}-3）}{3+4{k}^{2}}$，
由$\overrightarrow{MA}$=λ$\overrightarrow{A{F}_{2}}$，可得（x₁，y₁+k）=λ（1-x₁，-y₁），
∴$λ=\frac{{x}_{1}}{1-{x}_{1}}$，
由$\overrightarrow{MB}$=μ$\overrightarrow{B{F}_{2}}$，同理可得μ=$\frac{{x}_{2}}{1-{x}_{2}}$，
∴λ+μ=$\frac{{x}_{1}}{1-{x}_{1}}+\frac{{x}_{2}}{1-{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}-2{x}_{1}{x}_{2}}{1-（{x}_{1}+{x}_{2}）+{x}_{1}{x}_{2}}$=$\frac{\frac{8{k}^{2}}{3+4{k}^{2}}-\frac{8（{k}^{2}-3）}{3+4{k}^{2}}}{1-\frac{8{k}^{2}}{3+4{k}^{2}}+\frac{4（{k}^{2}-3）}{3+4{k}^{2}}}$=-$\frac{8}{3}$．
∴λ+μ=$-\frac{8}{3}$．
（III）①当直线l⊥x轴时，l的方程为：x=1．由$\left\{\begin{array}{l}{x=1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$，解得A$（1，\frac{3}{2}）$，B$（1，-\frac{3}{2}）$．
∴|AF₂|=|BF₂|=$\frac{3}{2}$，
∴|AF₂|+|BF₂|=3，|AF₂|•|BF₂|=$\frac{9}{4}$，
可得：|AF₂|+|BF₂|=$\frac{4}{3}$|AF₂|•|BF₂|．此时t=$\frac{4}{3}$．
②当直线l与x轴不垂直时，设l的方程为：y=k（x-1），
不妨设x₂＞1＞x₁，则|AF₂|=$\sqrt{（{x}_{1}-1）^{2}+{y}_{1}^{2}}$=$|{x}_{1}-1|•\sqrt{1+{k}^{2}}$，|BF₂|=$\sqrt{（{x}_{2}-1）^{2}+{y}_{1}^{2}}$=$|{x}_{2}-1|•\sqrt{1+{k}^{2}}$，
x₂-x₁=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{（\frac{8{k}^{2}}{3+4{k}^{2}}）^{2}-\frac{16（{k}^{2}-3）}{3+4{k}^{2}}}$=$\frac{12\sqrt{1+{k}^{2}}}{3+4{k}^{2}}$，
∴$\frac{1}{|A{F}_{2}|}+\frac{1}{|B{F}_{2}|}$=$\frac{1}{|{x}_{1}-1|\sqrt{1+{k}^{2}}}$+$\frac{1}{|{x}_{2}-1|\sqrt{1+{k}^{2}}}$
=$（\frac{1}{1-{x}_{1}}+\frac{1}{{x}_{2}-1}）•\frac{1}{\sqrt{1+{k}^{2}}}$
=$\frac{{x}_{2}-{x}_{1}}{{x}_{2}+{x}_{1}-{x}_{1}{x}_{2}-1}$$•\frac{1}{\sqrt{1+{k}^{2}}}$
=$\frac{\frac{12\sqrt{1+{k}^{2}}}{3+4{k}^{2}}}{\frac{8{k}^{2}}{3+4{k}^{2}}-\frac{4（{k}^{2}-3）}{3+4{k}^{2}}-1}$×$\frac{1}{\sqrt{1+{k}^{2}}}$=$\frac{4}{3}$．
即得：|AF₂|+|BF₂|=$\frac{4}{3}$|AF₂|•|BF₂|．
故存在实数t=$\frac{4}{3}$，使得|AF₂|+|BF₂|=$\frac{4}{3}$|AF₂|•|BF₂|．

点评 本题考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、向量坐标运算、弦长公式，考查了分类讨论思想方法、推理能力与计算能力，属于难题．