题目内容
14.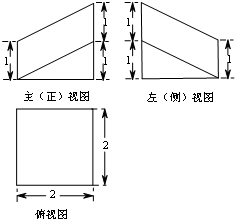 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )| A. | $\frac{10}{3}$ | B. | 3 | C. | $\frac{14}{3}$ | D. | 4 |
分析 首先根据三视图把几何体的复原图转换出来,进一步利用几何体的体积公式利用分割法求出结果.
解答 解:根据三视图得知:
该几何体是把一个一棱长为2的正方体,在右下边去除一个以底为直角三角形直角边长为2和1高为2的三棱柱,左上边去除一个以底为直角三角形直角边长为2和1高为2的三棱柱,
所以:V=V正方体-2V三棱柱
=8-2•$\frac{1}{2}•2•1•2$=4
故选:D.
点评 本题考查的知识要点:三视图与复原图的应用,几何体的体积公式的应用,主要考查学生的空间想象能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.已知向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$=(1,-2)的夹角为π,|$\overrightarrow{AB}$|=2$\sqrt{5}$,点A的坐标为(3,-4).则点B坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (5,-8) | D. | (-8,5) |
9.已知函数f(x)=sin(ωx+$\frac{π}{3}$)+$\sqrt{3}$sin(ωx-$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π,则( )
| A. | f(x)为偶函数 | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上单调递增 | ||
| C. | x=$\frac{π}{2}$为f(x)的图象的一条对称轴 | D. | ($\frac{π}{2}$,0)为f(x)的图象的一个对称中心 |
6.若x,y满足$\left\{\begin{array}{l}x+y≥0\\ x≥1\\ x-y≥0\end{array}\right.$,则下列不等式恒成立的是( )
| A. | y≥-1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
 中,内角
中,内角 ,
,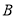 ,
,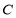 的对边分别为
的对边分别为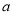 ,
,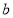 ,
,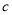 ,且
,且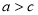 ,已知
,已知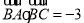 ,
,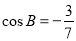 ,
,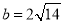 .求:
.求: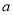 和
和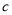 的值;
的值;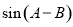 的值.
的值. 如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.
如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.