题目内容
7.已知一椭圆中心在坐标原点,左右焦点在x轴上,若其左焦点F1(-c,0)(c>0)到圆C:(x-2)2+(y-4)2=1上任意一点距离的最小值为4,且过椭圆右焦点F2(c,0)与上顶点的直线与圆O:x2+y2=$\frac{1}{2}$相切(Ⅰ)求椭圆E的方程;
(Ⅱ)若直线l:y=-x+m与椭圆E交于A、B两点,当以AB为直径的圆与y轴相切时,求△F1AB的面积.
分析 (Ⅰ)设出椭圆E的方程,由椭圆的右焦点到圆上任意一点的距离的最小值为4列式求得c,再写出过椭圆右焦点和上顶点的想方程,由直线和圆O相切列式求得b的值,结合隐含条件求出a,则椭圆E的方程可求;
(Ⅱ)联立直线方程和椭圆方程,化为关于x的一元二次方程后由△>0求得M的范围.利用弦长公式把圆的半径用含有m的代数式表示,由已知条件列式求得m的值,再求出点F1到直线AB的距离,然后对m分类求得△F1AB的面积.
解答 解:(Ⅰ)设椭圆E为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
焦点分别为F1(-c,0),F2(c,0),则椭圆的右焦点到圆上任意一点的距离的最小值为:
$\sqrt{(-c-2)^{2}+{4}^{2}}-1=4$,又c>0,∴c=1.
过椭圆右焦点和上顶点的想方程为$\frac{x}{1}+\frac{y}{b}=1$,即bx+y-b=0.
由直线和圆O相切可得$\frac{|-b|}{\sqrt{1+{b}^{2}}}=\frac{\sqrt{2}}{2}$,解得b=1,∴a2=b2+c2=2.
∴椭圆E的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=-x+m}\end{array}\right.$,可得3x2-4mx+2m2-2=0.
则△=(-4m)2-12(2m2-2)>0,即m2<3.
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=\frac{4m}{3},{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{3}$,
则AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}=\frac{2m}{3}$.
则以AB为直径的圆的半径为r=$\frac{1}{2}|AB|=\frac{\sqrt{2}}{2}|{x}_{1}-{x}_{2}|=\frac{\sqrt{2}}{2}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.
由条件可得$\frac{\sqrt{2}}{2}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}=|\frac{{x}_{1}+{x}_{2}}{2}|$.
整理可得$({x}_{1}+{x}_{2})^{2}=8{x}_{1}{x}_{2}$,即$(\frac{4m}{3})^{2}=8•\frac{2{m}^{2}-2}{3}$.
∴${m}^{2}=\frac{3}{2}<3$,解得$m=-\frac{\sqrt{6}}{2}$或$\frac{\sqrt{6}}{2}$.
此时,|AB|=$\sqrt{(1+1)({x}_{1}-{x}_{2})^{2}}=\sqrt{2[\frac{16{m}^{2}}{9}-\frac{4(2{m}^{2}-2)}{3}]}=\frac{2\sqrt{6}}{3}$.
点F1到直线AB的距离为d=$\frac{|-1-m|}{\sqrt{2}}$,
∴当m=$\frac{\sqrt{6}}{2}$时,△F1AB的面积为S=$\frac{1}{2}|AB|•d=\frac{\sqrt{6}}{3}×\frac{1}{\sqrt{2}}(1+\frac{\sqrt{6}}{2})=\frac{3\sqrt{2}+2\sqrt{3}}{6}$.
当m=$-\frac{\sqrt{6}}{2}$时,△F1AB的面积为S=$\frac{\sqrt{6}}{3}×\frac{1}{\sqrt{2}}(-1+\frac{\sqrt{6}}{2})=\frac{3\sqrt{2}-2\sqrt{3}}{6}$.
点评 本题考查了椭圆方程的求法,考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是压轴题.

| A. | $\frac{16\sqrt{6}}{3}$ | B. | 8 | C. | $\frac{5\sqrt{15}}{3}$ | D. | 6 |
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
 ,
, .
. 的解集为
的解集为 ,求
,求 的值;
的值; ,使
,使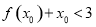 ,求
,求 的取值范围.
的取值范围.