题目内容
(本小题满分12分)
设函数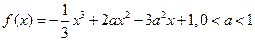 。
。
(1)求函数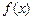 的极大值;
的极大值;
(2)若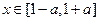 时,恒有
时,恒有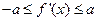 成立(其中
成立(其中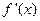 是函数
是函数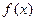 的导函数),试确定实数
的导函数),试确定实数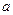 的取值范围。
的取值范围。
设函数
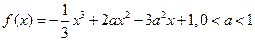 。
。(1)求函数
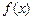 的极大值;
的极大值;(2)若
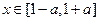 时,恒有
时,恒有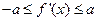 成立(其中
成立(其中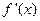 是函数
是函数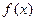 的导函数),试确定实数
的导函数),试确定实数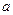 的取值范围。
的取值范围。(1)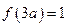
(2)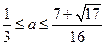
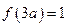
(2)
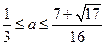
(1)∵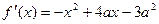 ,且
,且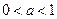 , ……1分
, ……1分
当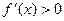 时,得
时,得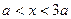 ;当
;当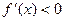 时,得
时,得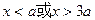 ;
;
∴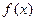 的单调递增区间为
的单调递增区间为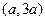 ;
;
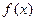 的单调递减区间为
的单调递减区间为 和
和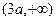 . ……3分
. ……3分
故当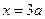 时,
时,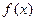 有极大值,其极大值为
有极大值,其极大值为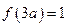 . ……4分
. ……4分
(2)∵ ,
,
①当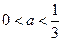 时,
时,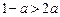 ,
,
∴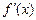 在区间
在区间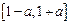 内是单调递减.
内是单调递减.
∴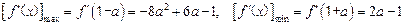 .
.
∵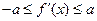 ,∴
,∴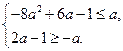
此时,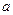 不存在. ……8分
不存在. ……8分
②当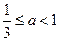 时,
时,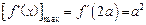 .
.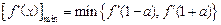
∵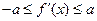 ,∴
,∴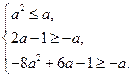 即
即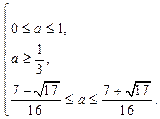
此时,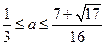 .
.  ……12分
……12分
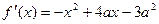 ,且
,且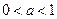 , ……1分
, ……1分当
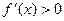 时,得
时,得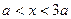 ;当
;当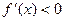 时,得
时,得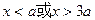 ;
;∴
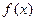 的单调递增区间为
的单调递增区间为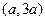 ;
;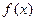 的单调递减区间为
的单调递减区间为 和
和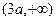 . ……3分
. ……3分故当
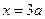 时,
时,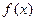 有极大值,其极大值为
有极大值,其极大值为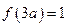 . ……4分
. ……4分(2)∵
 ,
,①当
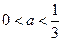 时,
时,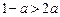 ,
,∴
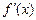 在区间
在区间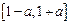 内是单调递减.
内是单调递减.∴
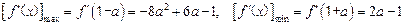 .
.∵
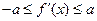 ,∴
,∴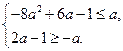
此时,
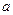 不存在. ……8分
不存在. ……8分②当
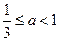 时,
时,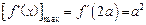 .
.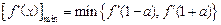
∵
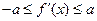 ,∴
,∴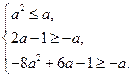 即
即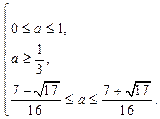
此时,
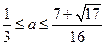 .
.  ……12分
……12分
练习册系列答案
相关题目
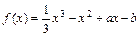 ,
,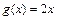 ,当
,当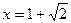 时,
时,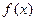 取得极值。
取得极值。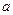 的值;
的值;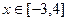 时,函数
时,函数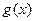 的图象有三个公共点,求
的图象有三个公共点,求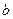 的取值范围。
的取值范围。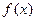 =
=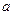
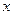 -
-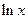 ,
,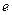 是自然常数,
是自然常数,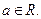
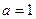 时, 求
时, 求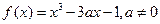 .
.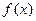 的单调区间;
的单调区间; 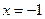 处取得极值,直线
处取得极值,直线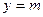 与
与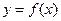 的图象有三个不同的交点,求
的图象有三个不同的交点,求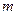 的取值范围。
的取值范围。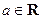 ,若函数
,若函数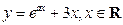 有大于零的极值点,则
有大于零的极值点,则



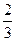 与
与 x=1时都取得极值.
x=1时都取得极值. 。
。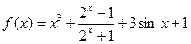 在区间[
在区间[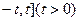 上的最大值与最小值的和 .
上的最大值与最小值的和 .