题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() 与6的等差中项为
与6的等差中项为![]() .数列
.数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】见解析
【解析】(Ⅰ)由已知当![]() 时,
时,![]() ,整理得
,整理得![]() ,
,
所以数列![]() 从第2项起构成等差数列,公差
从第2项起构成等差数列,公差![]() .
.
而![]() ,
,
故当![]() 时,
时,![]() . ----------------------2分
. ----------------------2分
而![]() ,显然
,显然![]() ,
,
故![]() . ------------------4分
. ------------------4分
等比数列![]() 中,
中,![]() ,
,![]() ,故其公比
,故其公比![]() .
.
所以其通项![]() . ---------------------------6分
. ---------------------------6分
(Ⅱ)令![]() ,由(Ⅰ)知,
,由(Ⅰ)知,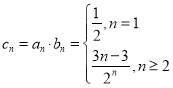 . ---------------7分
. ---------------7分
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() ①
①
![]() ②
②
①![]() ②,得
②,得
![]()
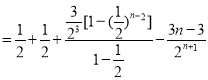
![]()
![]() ,
,
所以![]() . -------------------11分
. -------------------11分
显然,当![]() 时,也成立.
时,也成立.
故![]() . -------------------12分
. -------------------12分
【命题意图】本题考查![]() 与
与![]() 的关系、等比数列的基本运算、数列通项公式以及数列求和等,考查基本的运算能力与逻辑推理能力等.
的关系、等比数列的基本运算、数列通项公式以及数列求和等,考查基本的运算能力与逻辑推理能力等.

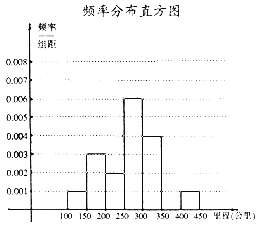
【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组 | 频数 | 频率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合计 | N | 1 |
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.