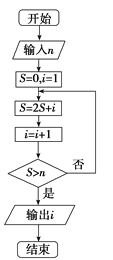
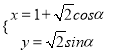题目内容
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知由1,2,3号三位男性选手和4,5号两位女性选手组成混合组参赛.已知象棋大赛共有三轮,设三位男性选手在一至三轮胜出的概率依次是![]() ;两名女性选手在一至三轮胜出的概率依次是
;两名女性选手在一至三轮胜出的概率依次是![]() .
.
(Ⅰ)若该组五名选手与另一组选手进行小组淘汰赛,每名选手只比赛一局,共五局比赛,求该组两名女性选手的比赛次序恰好不相邻的概率;
(Ⅱ)若一位男性选手因身体不适退出比赛,剩余四人参加个人比赛,比赛结果相互不影响,设![]() 表示该组选手在四轮中胜出的人数,求随机变量
表示该组选手在四轮中胜出的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】见解析
【解析】(Ⅰ)记两名女性选手比赛次序恰好不相邻为事件![]() .
.
则五人不同的比赛次序为![]() 种;
种;
事件![]() 对应的比赛次序为
对应的比赛次序为![]() 种.
种.
所以![]() . -----------------------------5分
. -----------------------------5分
(Ⅱ)男性选手在三轮中胜出的概率为![]() ;
;
两名女性选手在三轮中胜出的概率为![]() . -----------------------------6分
. -----------------------------6分
由题意可知男性选手三轮中胜出的人数![]() ;女性选手三轮比赛中胜出的人数
;女性选手三轮比赛中胜出的人数![]() ,显然
,显然![]() . -----------------------------7分
. -----------------------------7分
所以![]() 可取
可取![]() .
.
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]() . -----------------------------10分
. -----------------------------10分
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
-----------------------------11分
所以![]() . -----------------------------12分
. -----------------------------12分
另,![]() .
.
【命题意图】本题考查古典概型的求解、相互独立事件与独立重复实验的概率求解、离散型随机变量的分布列及其数学期望的求解等,意在考查基本的运算能力、逻辑推理能力和数学应用意识等.

【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据![]() ;
;
(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.