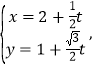题目内容
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 。
。
【解析】分析:(Ⅰ)由题意可得在在直角三角形![]() 中有
中有![]() ,即
,即![]() ,整理可得
,整理可得![]() .(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=
.(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]()
=2c,根据直线![]() 与圆相切可得
与圆相切可得![]() ,解得c=1,从而
,解得c=1,从而![]() ,
,![]() ,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为
,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为![]() ,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为
,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为![]() ,若以PM,PN为邻边的平行四边形是菱形,则
,若以PM,PN为邻边的平行四边形是菱形,则![]() ,由此得到
,由此得到![]() ,整理得
,整理得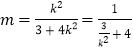 ,最后可求得
,最后可求得![]() .
.
详解:(I)∵AB⊥AF2,![]() 为
为![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即椭圆C的离心率为![]() .
.
(II)过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]() =2c.
=2c.
∵直线![]() :
:![]() 相切,
相切,
∴![]() ,
,
解得c=1.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴椭圆C的方程为![]() .
.
(III)由(I)知,F2(1,0),直线MN的方程为![]() ,
,
由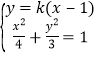 消去y整理得
消去y整理得![]()
∵直线与椭圆C交于M,N两点,
∴![]() .
.
设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
则![]()
∴![]() ,
,
∴MN的中点Q的坐标为![]() ,
,
若以PM,PN为邻边的平行四边形是菱形,
则![]() ,
,
∴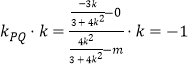
整理得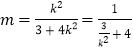 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
故存在满足题意的点P,且m的取值范围是(![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目