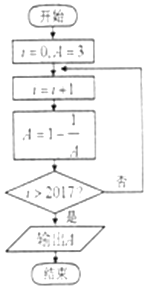
题目内容
【题目】在正三棱柱ABC﹣A1B1C1中,AB=2,AA1=3,点D为BC的中点;
(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)若点E为A1C上的点,且满足 ![]() =m
=m ![]() (m∈R),若二面角E﹣AD﹣C的余弦值为
(m∈R),若二面角E﹣AD﹣C的余弦值为 ![]() ,求实数m的值.
,求实数m的值.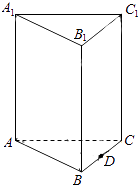
【答案】证明:(Ⅰ)连结A1C∩AC1于F,则F为AC1的中点,
连结DF,则A1B∥DF,
∵DF平面AC1D,∴A1B∥平面AC1D.
解:(Ⅱ)过E作EM⊥AC于M,则EM⊥平面ABC,过M作MN⊥AD,垂足为N,连结EN,
则EN⊥AD,∴∠ENM为二面角E﹣AD﹣C的一个平面角,
设EM=h,则 ![]() =
= ![]() ,∴CM=
,∴CM= ![]() ,∴AM=2﹣
,∴AM=2﹣ ![]() ,
,
∵ ![]() ,∴MN=
,∴MN= ![]() ,
,
∴EN2=EM2+MN2=h2+(1﹣ ![]() )2 ,
)2 ,
∵cos ![]() ,故
,故 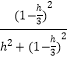 =
= ![]() ,解得h=
,解得h= ![]() ,
,
此时,点E为A1C的中点,∴m=1.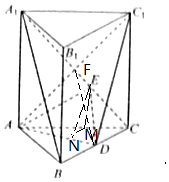
【解析】(Ⅰ)连结A1C∩AC1于F,则F为AC1的中点,连结DF,则A1B∥DF,由此能证明A1B∥平面AC1D.(Ⅱ)过E作EM⊥AC于M,则EM⊥平面ABC,过M作MN⊥AD,垂足为N,连结EN,则∠ENM为二面角E﹣AD﹣C的一个平面角,由此利用二面角E﹣AD﹣C的余弦值为 ![]() ,能求出m的值.
,能求出m的值.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目