题目内容
【题目】已知圆C：（x﹣ 
）2+（y﹣1）2=1和两点A（﹣t，0），B（t，0）（t＞0），若圆C上存在点P，使得∠APB=90°，则当t取得最大值时，点P的坐标是（ ）
A.（ 
， 
）
B.（ ， ）
C.（ ， 
）
D.（ ， ）
【答案】D
【解析】解：圆C：（x﹣ 
）2+（y﹣1）2=1，其圆心C（ ，1），半径为1，
∵圆心C到O（0，0）的距离为2，
∴圆C上的点到点O的距离的最大值为3．
再由∠APB=90°，以AB为直径的圆和圆C有交点，可得PO= 
AB=t，故有t≤3，
∴A（﹣3，0），B（3，0）．
∵圆心C（ ，1），直线OP的斜率k= 
，
∴直线OP的方程为y= 
联立：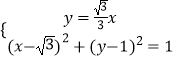 
解得：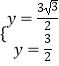 
．
故选D．
根据圆心C到O（0，0）的距离为2，可得圆C上的点到点O的距离的最大值为3．再由∠APB=90°，可得PO= AB=t，可得t≤3，从而得到答案．
练习册系列答案
相关题目
