题目内容
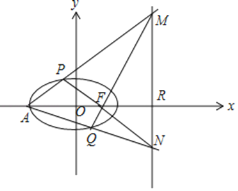
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两个动点,直线
的两个动点,直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(I)求椭圆![]() 的方程;
的方程;
(II)若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求
,求![]() 的坐标;
的坐标;
(III)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 三点共线,求证:
三点共线,求证:![]() .
.
【答案】(I)![]() (II)
(II)![]() 的坐标为
的坐标为![]() 或
或![]() .(III)见解析
.(III)见解析
【解析】
(Ⅰ)由题意得c=1,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;(Ⅱ)由△PAF与△PMF的面积之比为![]() ,可得
,可得![]() .设M(4,m)(m≠0),P(x0,y0),则
.设M(4,m)(m≠0),P(x0,y0),则![]() ,求得
,求得![]() .将其代入
.将其代入![]() ,解得m=±9.则M的坐标可求;(Ⅲ)设M(4,m),N(4,n),P(x0,y0),分析可得m≠0,n≠0.直线AM的方程为
,解得m=±9.则M的坐标可求;(Ⅲ)设M(4,m),N(4,n),P(x0,y0),分析可得m≠0,n≠0.直线AM的方程为![]() .联立直线方程与椭圆方程,利用根与系数的关系求得P的坐标,利用利用对称性证明若P,F,Q三点共线,则∠MFR=∠FNR.
.联立直线方程与椭圆方程,利用根与系数的关系求得P的坐标,利用利用对称性证明若P,F,Q三点共线,则∠MFR=∠FNR.
(I)由题意得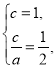 解得
解得![]()
因为![]() ,所以
,所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(II)因为![]() 与
与![]() 的面积之比为
的面积之比为![]() ,
,
所以![]() .
.
所以![]() .
.
设![]() ,则
,则![]() ,
,
解得![]() .
.
将其代入![]() ,解得
,解得![]() .
.
所以![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(III)设![]() ,
,
若![]() ,则
,则![]() 为椭圆
为椭圆![]() 的右顶点,由
的右顶点,由![]() 三点共线知,
三点共线知,![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,
不符合题意.
所以![]() .同理
.同理![]() .
.
直线![]() 的方程为
的方程为![]() .
.
由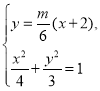 消去
消去![]() ,整理得
,整理得![]() .
.
![]() 成立.
成立.
由![]() ,解得
,解得![]() .
.
所以![]() .
.
所以![]() .
.
当![]() 时,
时,![]() ,
,![]() ,即直线
,即直线![]() 轴.
轴.
由椭圆的对称性可得![]() .
.
又因为![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() ,
,
直线![]() 的斜率
的斜率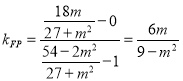 .
.
同理![]() .
.
因为![]() 三点共线,
三点共线,
所以![]() .
.
所以![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
所以![]() .
.
因为![]() 均为锐角,
均为锐角,
所以![]() .
.
综上,若![]() 三点共线,则
三点共线,则![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目